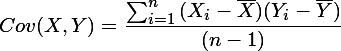主成分分析PCA工作原理和简单介绍
PCA原理:
PCA的原理就是将原来的样本数据投影到一个新的空间中,相当于我们在矩阵分析里面学习的将一组矩阵映射到另外的坐标系下。通过一个转换坐标,也可以理解成把一组坐标转换到另外一组坐标系下,但是在新的坐标系下,表示原来的原本不需要那么多的变量,只需要原来样本的最大的一个线性无关组的特征值对应的空间的坐标即可。
比如,原来的样本是30*1000000的维数,就是说我们有30个样本,每个样本有1000000个特征点,这个特征点太多了,我们需要对这些样本的特征点进行降维。那么在降维的时候会计算一个原来样本矩阵的协方差矩阵,这里就是1000000*1000000,当然,这个矩阵太大了,计算的时候有其他的方式进行处理,这里只是讲解基本的原理,然后通过这个1000000*1000000的协方差矩阵计算它的特征值和特征向量,最后获得具有最大特征值的特征向量构成转换矩阵。比如我们的前29个特征值已经能够占到所有特征值的99%以上,那么我们只需要提取前29个特征值对应的特征向量即可。这样就构成了一个1000000*29的转换矩阵,然后用原来的样本乘以这个转换矩阵,就可以得到原来的样本数据在新的特征空间的对应的坐标。30*1000000 * 1000000*29 = 30 *29, 这样原来的训练样本每个样本的特征值的个数就降到了29个。
一般来说,PCA降维后的每个样本的特征的维数,不会超过训练样本的个数,因为超出的特征是没有意义的。
下面是百度百科中对pca降维的一段解释,还是挺清晰的:
“对于一个训练集,100个对象模板,特征是10维,那么它可以建立一个100*10的矩阵,作为样本。求这个样本的协方差矩阵,得到一个10*10的协方差矩阵,然后求出这个协方差矩阵的特征值和特征向量,应该有10个特征值和特征向量,我们根据特征值的大小,取前四个特征值所对应的特征向量,构成一个10*4的矩阵,这个矩阵就是我们要求的特征矩阵,100*10的样本矩阵乘以这个10*4的特征矩阵,就得到了一个100*4的新的降维之后的样本矩阵,每个特征的维数下降了。
当给定一个测试的特征集之后,比如1*10维的特征,乘以上面得到的10*4的特征矩阵,便可以得到一个1*4的特征,用这个特征去分类。”
降维的必要性
1.多重共线性--预测变量之间相互关联。多重共线性会导致解空间的不稳定,从而可能导致结果的不连贯。
2.高维空间本身具有稀疏性。一维正态分布有68%的值落于正负标准差之间,而在十维空间上只有0.02%。
3.过多的变量会妨碍查找规律的建立。
4.仅在变量层面上分析可能会忽略变量之间的潜在联系。例如几个预测变量可能落入仅反映数据某一方面特征的一个组内。
降维的目的:
1.减少预测变量的个数
2.确保这些变量是相互独立的
3.提供一个框架来解释结果
降维的方法有:主成分分析、因子分析、用户自定义复合等。
PCA(Principal Component Analysis)不仅仅是对高维数据进行降维,更重要的是经过降维去除了噪声,发现了数据中的模式。
PCA把原先的n个特征用数目更少的m个特征取代,新特征是旧特征的线性组合,这些线性组合最大化样本方差,尽量使新的m个特征互不相关。从旧特征到新特征的映射捕获数据中的固有变异性。
预备知识
样本X和样本Y的协方差(Covariance):
协方差为正时说明X和Y是正相关关系,协方差为负时X和Y是负相关关系,协方差为0时X和Y相互独立。
Cov(X,X)就是X的方差(Variance).
当样本是n维数据时,它们的协方差实际上是协方差矩阵(对称方阵),方阵的边长是![]() 。比如对于3维数据(x,y,z),计算它的协方差就是:
。比如对于3维数据(x,y,z),计算它的协方差就是:
若![]() ,则称
,则称![]() 是A的特征值,X是对应的特征向量。实际上可以这样理解:矩阵A作用在它的特征向量X上,仅仅使得X的长度发生了变化,缩放比例就是相应的特征值
是A的特征值,X是对应的特征向量。实际上可以这样理解:矩阵A作用在它的特征向量X上,仅仅使得X的长度发生了变化,缩放比例就是相应的特征值![]() 。
。
当A是n阶可逆矩阵时,A与P-1Ap相似,相似矩阵具有相同的特征值。
特别地,当A是对称矩阵时,A的奇异值等于A的特征值,存在正交矩阵Q(Q-1=QT),使得:
对A进行奇异值分解就能求出所有特征值和Q矩阵。
![]() D是由特征值组成的对角矩阵
D是由特征值组成的对角矩阵
由特征值和特征向量的定义知,Q的列向量就是A的特征向量。
Jama包
Jama包是用于基本线性代数运算的java包,提供矩阵的cholesky分解、LUD分解、QR分解、奇异值分解,以及PCA中要用到的特征值分解,此外可以计算矩阵的乘除法、矩阵的范数和条件数、解线性方程组等。
PCA过程
1.特征中心化。即每一维的数据都减去该维的均值。这里的“维”指的就是一个特征(或属性),变换之后每一维的均值都变成了0。
很多数据挖掘的教材上都会讲到鹫尾花的例子,本文就拿它来做计算。原始数据是150×4的矩阵A:
每一列减去该列均值后,得到矩阵B:
2.计算B的协方差矩阵C:
4.2248414 0 0 0
0 0.24224437 0 0
0 0 0.078524387 0
0 0 0 0.023681839
V=
0.36158919 0.65654382 -0.58100304 0.3172364
-0.082268924 0.72970845 0.596429220 -0.3240827
0.85657212 -0.17576972 0. 072535217 -0.47971643
0.35884438 -0.074704743 0.54904125 0.75113489
每个样本正好是二维的,画在平面坐标系中如图:
鹫尾花数据集共分为3类花(前50个样本为一类,中间50个样本为一类,后50个样本为一类),从上图可以看到把数据集映射到2维后分类会更容易进行,直观上看已经是线性可分的了,下面我们用自组织映射网络对其进行聚类。
当然我们已知了有3类,所以在设计SOFM网络时,我把竞争层节点数设为3,此时的聚类结果是前50个样本聚为一类,后100个样本聚为一类。当把竞争层节点数改为4时,仅第2类中的3个样本被误分到了第3类中,整体精度达98%!
输出聚类结果:
http://www.cnblogs.com/zhangchaoyang/articles/2222048.html