算法学习笔记（四） KMP算法之 next 数组详解

最近回顾了下字符串匹配 KMP 算法，相对于朴素匹配算法，KMP算法核心改进就在于：待匹配串指针 i 不发生回溯，模式串指针 j 跳转到 next[j]，即变为了 j = next[j]. 由此时间复杂度由朴素匹配的 O(m*n) 降到了 O(m+n), 其中模式串长度 m, 待匹配文本串长 n.

其中，比较难理解的地方就是 next 数组的求法。next 数组的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀，也可看作有限状态自动机的状态，而且从自动机的角度反而更容易推导一些。

• "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；
• "后缀"则指除了第一个字符以外，一个字符串的全部尾部组合。

next 数组推导

求 next 数组用到了递推，算法的构建思想就是：
已知初始 next[0] = -1, next[j] = k, 来求 next[j+1] 是多少，有点儿像数学归纳法的套路。
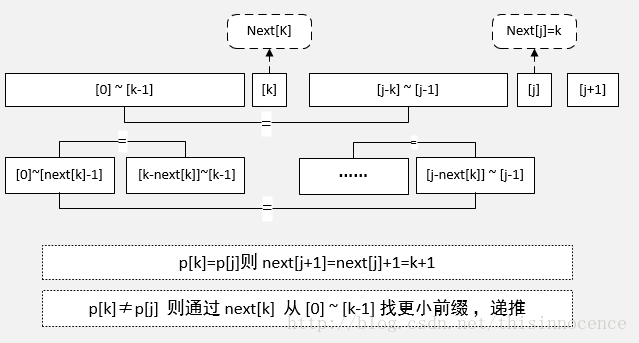
由 next[j] = k, 我们知道 p[k-1] = p[j-1], 前缀 [0] ~ [k-1] ， 后缀则从 [j-k] ~ [j-1], 长度都为 k。接下来 next[j+1] 求法就分两种情况讨论：

如果 p[k]  = p[j], 很显然 next[j+1] = next[j] + 1 = k+1;

如果 p[k] != p[j], 那么说明匹配的前后缀更短，前缀里要找一个最后字符 p[k'] = p[j], 前缀再往前推, 同时要保证 [0] ~ [k'] = [j-k'] ~ [j]，k'+ 1 就是要求的 next[j+1]. 这个符合条件的 k' 要怎么推，由 k 依次递减吗？显然不是，是由 k=next[k] 的往前跳;

由 next[j]=k ,我们已知了 [0] ~ [k-1] 等于 [j-k] ~ [j-1], 那么下一步我们在 [0] ~ [k-1] 中取最大匹配的前后缀，其正好可由 next[k] 求出，即：[0]~[next[k]-1] 等于 [k-next[k]]~[k-1], 有 next[k] 个字符匹配。

因为 [0] ~ [k-1] 等于 [j-k] ~[j-1], 所以在 [j-k] ~ [j-1] 也存在同样的最大前后缀匹配，我们取 [0] ~ [k-1] 中的前缀 [0]~[next[k]-1]， [j-k] ~ [j-1] 中的后缀 [j-next[k]] ~ [j-1],它们必然相等，然后再进一步判断 p[j] 是否等于 p[next[k]] 即可，由此递推完成匹配 p[k']=p[j] 或者 递推到了 k=next[0]=-1 结束。

这种思路直接转换为代码就是：

void GetNext(char *p, int *next) {
    next[0] = -1;
    int pLen = strlen(p), j, k;
    for (j = 0; j < pLen - 1; j++) {
        k = next[j];
        while (k != -1 && p[k] != p[j]){
            k = next[k];          // 在前缀里找 p[k'] = p[j]，前缀=后缀，前缀的前缀 = 后缀的后缀，递推。
        }
        next[j + 1] = k + 1;      // 如果递推到了 next[0], 无匹配为0；递推找到 p[k']=p[j], next[j+1] = next[k']+1
    }
}

代码思路不变，进行一下优化：

void GetNext2(char *p, int *next) { 
    next[0] = -1;
    int j = 0, k = -1, pLen = strlen(p);
    while (j < pLen - 1) {
        if (k != -1 && p[k] != p[j])
            k = next[k];
        else
            next[++j] = ++k;     // <=> {++j; ++k; next[j] = next[k]}
    }
}

优化 next 数组

上面的 next 数组应用到模版串和待匹配串的匹配时还是存在多余的跳转，进行一步判断优化即可，解释见代码中的注释：

void GetNextVal(char *p, int *next) {
    next[0] = -1;
    int j = 0, k = -1, pLen = strlen(p);
    while (j < pLen - 1) {
        if (k != -1 && p[k] != p[j]) {
            k = next[k];
        } else {
            if (p[++k] != p[++j])
                next[j] = k;
            else
                next[j] = next[k]; // 比较前面改进相当于这里 next[j] = k 变为 next[j] = next[k], 多递推一次
        }                          // kmp 比较 s[i] != p[j], p[j] 跳到 p[next[j]], 而 p[j] = p[next[j]], 故多递推一次
    }
}

KMP 匹配主算法

int KmpSearch(char *s, char *p, int *next) {
    int sLen = strlen(s);
    int pLen = strlen(p);
    int i = 0, j = 0;
    while (i < sLen && j < pLen) {
        if (j == -1 || s[i] == p[j]) {     // 相对于朴素匹配，多判断下 j == -1, 因为 next[0]=-1
            i++;
            j++;
        } else {
            j = next[j];                 // 相对于朴素匹配，没有了指针 i 的回溯，j 跳转到 next[j]
        }
    }
    if (j == pLen)
        return i - j;
    else
        return -1;
}

小实验(C实现)

#include <stdio.h>
#include <string.h>

void GetNext(char *p, int *next) {
	next[0] = -1;
	int j = 0, k = -1, pLen = strlen(p);
	while (j < pLen - 1) {
		if (k != -1 && p[k] != p[j])
			k = next[k];
		else
			next[++j] = ++k;
	}
}

void GetNext2(char *p, int *next) {
	next[0] = -1;
	int pLen = strlen(p), j, k;
	for (j = 0; j < pLen - 1; j++) {
		k = next[j];
		while (k != -1 && p[k] != p[j]){
			k = next[k];
		}
		next[j + 1] = k + 1;
	}
}

void GetNextVal(char *p, int *next) {
	next[0] = -1;
	int j = 0, k = -1, pLen = strlen(p);
	while (j < pLen - 1) {
		if (k != -1 && p[k] != p[j]) {
			k = next[k];
		} else {
			if (p[++k] != p[++j])
				next[j] = k;
			else
				next[j] = next[k];
		}
	}
}

int KmpSearch(char *s, char *p, int *next) {
	int sLen = strlen(s);
	int pLen = strlen(p);
	int i = 0, j = 0;
	while (i < sLen && j < pLen) {
		if (j == -1 || s[i] == p[j]) { // 相对于朴素匹配，多判断下 j == -1, 因为 next[0]=-1
			i++;
			j++;
		} else {
			j = next[j]; // 相对于朴素匹配，没有了指针 i 的回溯，j 跳转到 next[j]
		}
	}
	if (j == pLen)
		return i - j;
	else
		return -1;
}

int main() {
	char *s = "BBC ABCDAB ABCDABCDABDE";
	char *p = "ABCDABD";
	int n = strlen(p);
	int next[n], next2[n], nextVal[n];
	int index, indexVal, i;

	GetNext(p, next);
	index = KmpSearch(s, p, next);

	GetNext2(p, next2);

	GetNextVal(p, nextVal);
	indexVal = KmpSearch(s, p, nextVal);

	for (i = 0; i < n; i++)
		printf("%d\t", next[i]);
	printf("\n");

	for (i = 0; i < n; i++)
		printf("%d\t", next2[i]);
	printf("\n");

	for (i = 0; i < n; i++)
		printf("%d\t", nextVal[i]);
	printf("\n");

	printf("%d\t%d", index, indexVal);
	return 0;
}

/* 输出：
-1	0	0	0	0	1	2	
-1	0	0	0	0	1	2	
-1	0	0	0	-1	0	2	
15	15
 */

总结

KMP 算法用到的是 动态规划 的思想，按照步骤自己推导一遍会发现其实也并不是很难理解，自己一定要一步一步的推导一遍，观察每一步到底发生了什么。运用有限状态自动机来解决字符匹配会更加的方便，通用性也会更强。

【原文地址】：http://blog.csdn.net/thisinnocence