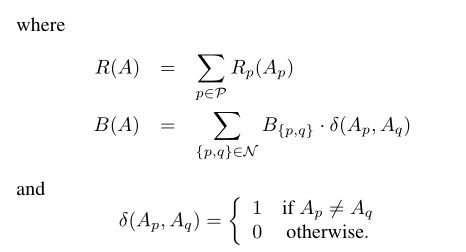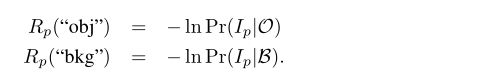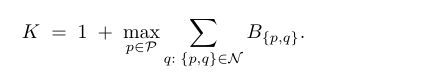Graph Cuts
Graph Cuts 是Yuri Y. Boykov 和 Marie-Pierre Jolly 发表在2001年iccv 上一篇论文提出的方法。他们研究,用一种交互式的方式来进行图像的分割。先由用户标记一些背景或者物体的种子像素点,然后用Graph Cuts的方法进行分割。
Graph cuts是一种十分有用和流行的能量优化算法,在计算机视觉领域普遍应用于前背景分割(Image segmentation)、立体视觉(stereo vision)、抠图(Image matting)等。[6]
理论
cost function 是一个能量函数。
而图像分割的问题在于将像素标记为“obj”还是“bkg”(分别表示object 和 background )。这个过程可以通过先将图像建立为图(图论中的图,而非图片的图),然后使用最大流/最小割的方法来完成。
那我们的目标就是想要在目标和背景的边界处割开,同时,这时候的能量也应该是最小的。[6]
在论文中,提出,若 A 代表如下:
A = (A 1 ,…,A p ,…,A |P| )
其中 Ap 对应到每个像素的label,它的值是“obj”或者“bkg” (表示物体和背景)。

那么图像分割时,cost function E 的表示如下:
E(A) = λ · R(A) + B(A)
R(A) 与 B(A)
R(A) 表示的是区域项,B(A) 表示的是边界项,而![]() 就是它们之间的重要因子,决定它们对能量的影响大小。[6]
就是它们之间的重要因子,决定它们对能量的影响大小。[6]
如果![]() 为0 ,那么只考虑边界而不考虑区域。这个影响的效果在后文中,将以实验结果的形式给出对比。
为0 ,那么只考虑边界而不考虑区域。这个影响的效果在后文中,将以实验结果的形式给出对比。
Graph Cuts 的目标是让E的结果最小。
将图像转化为G(V, E)
在与最小割的方法相关联之前,先将图像转化为无向图G(V,E)。其中V 表示顶点,E 表示边。
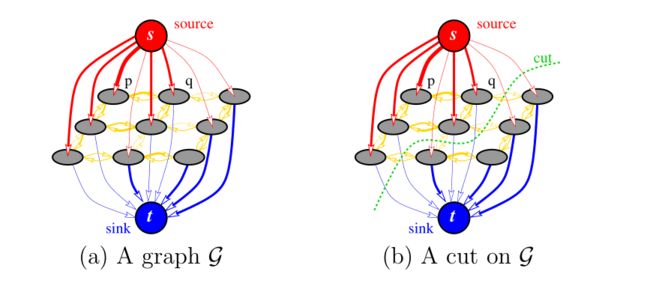
(图像来源[7])
Graph Cuts 建立的图中,除了每个像素点都作为一个单独的顶点外,还有多出了两个特殊的点S 和 T (源点和汇点)。
这两个顶点与每个像素点都连接起来。S 只有输出边(前向边),T只有输入边(后向边)。
而每个像素点与它的四邻域点之间都有边,这些是无向边,那么转化为有向边的最小割问题时,就将无向边分为两条成环的有向边了。
在图中有两种link:
- n-links,普通像素点之间的连接
- t-links,S 和T 连接每个像素点的边
这两种边、S、T和每个像素点组成了一个图。
接下来就是用最小割算法,计算得出最小的割。
建立无向图时的计算公式
对于图像的cost function
cost function 的计算如下表:
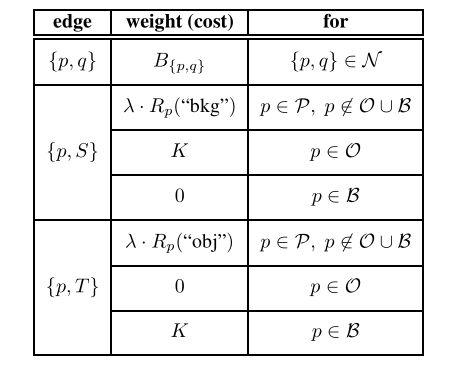
其中各个计算的方式在下文写着。
B{p, q} 正比于一个指数函数。可以看到 (p,q) 和 (q,p) 的权值是一样的。
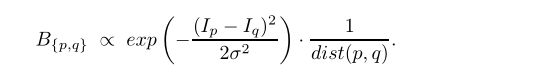
正比系数可以为1。
其中 O 和 B 分别表示 object 和 background
Pr(Ip | O) 表示像素点 Ip 是object 的概率
Pr( Ip | B) 表示像素点 Ip 是background 的概率。
在进行图像分割之前,由用户手动标记出一些背景和目标的像素点(交互式),大概如下:

(图像来源[2] )
那么,标记出像素点后就可以统计直方图了,则关于概率的计算如下:
对于一个给定的像素 Ip , N(po) 表示object 中的个数,
N(pb) 表示background 中的个数,则两个概率的计算分别是:
po = N(po)/( N(po)N(pb) )
pb = N(pb)/( N(po)N(pb) )
total = po+pb;
po /= total, pb /= total;//最后这两步为了避免某一方面的标记数量过多
//而带来的数据偏差,在实际的实现中,需要特别注意,不要除以0了两个尚不确定的参数
![]() 和
和 ![]() 在论文中,并没有给出特定的某个测试值,所以在实现的时候,自己慢慢调一下参数吧,看看效果如何
在论文中,并没有给出特定的某个测试值,所以在实现的时候,自己慢慢调一下参数吧,看看效果如何
在初始的计算中,两个参数分别如下:
lambda = 1.0f;
keno = 1.0f;算出cost function 之后,就可以使用最大流\最小割算法了。
就以上的分析,可以看到,对于n-links,
当两个未知标记的像素点的值很接近时,它们之间的边cost 越大
如果值差别很大,那么cost 越小,越有可能被分割
而对应于t-links
在与S 的连接中:
如果像素点标记为 “obj“,那么cost 是 max(B{p,q}),最不可能被分割
如果像素点标记为”bkg“,那么cost 为0,一定被分割
如果像素点未知,那么当它属于”bkg“的概率越大,cost越小,越有可能被分割
而在于T 的连接中,分析差不多。
实现
整篇大致分为两部分:计算cost 和 最小割算法。
数据结构的定义
像素与像素之间的关系是非常明确而有规律的,仔细分析,可以得到以下规律(边界点除外)
每个点都有五条输出的边和五条输入的边
输出的边是每个点的四邻域像素和一个源点(S)
输入的边是每个点的四邻域像素和一个汇点(T)
所以,每个像素点,可以包含五条输出的边。
struct Edge
{
float ca, float f;//容量和流量
};
struct Pixel
{
int i;//表示像素的坐标,由于我的个人习惯,我喜欢用一维的数组映射像素坐标
int edgeIndex[5];//9条边的记录
};
Edge S[N];//N 是像素的总数,表示S 点到各个像素点的边
//如果要找输入的边,那么通过像素的关系,就可以很容易的映射回来了
//and ,我更喜欢通过下标来映射各自的关系,所以实际实现应该略有不同最大流/最小割算法
有两个经典的算法,一个是Ford-Fulkerson算法(增广路径)[5]
一个是Push–relabel 算法[6]
然而作者在04年也发表了一种针对Graph Cuts 的算法[7],与传统的算法做了比较
结果
如果lambda 的值越大,算法跑的时间越长(因为要考虑到区域项的影响),下面给出lambda 为1和为0 的两种结果对比:
*代码可在github 上获得xiaosa233
(Compute Vision/Graph Cuts)
【参考资料】
[1] Boykov Y Y, Jolly M P. Interactive graph cuts for optimal boundary & region segmentation of objects in ND images[C]//Computer Vision, 2001. ICCV 2001. Proceedings. Eighth IEEE International Conference on. IEEE, 2001, 1: 105-112.
[2] 郭振锋. 基于 Graph Cuts 的交互式图像分割[D]. 中南大学, 2013.
[3] Push–relabel maximum flow algorithm
[4] The push-relabel algorithm
[5] [原创]最大流/最小割(maxflow/mincut)的原理讲解和代码实现_小腹黑zju_新浪博客
[6] 图像分割之(二)Graph Cut(图割) - zouxy09的专栏
[7] Boykov Y, Kolmogorov V. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2004, 26(9): 1124-1137.
如有错误,不足之处,欢迎提出,与君共勉
–END–