Image Warping
这次的这个小任务花了很长时间,现在回头看看,之前之所以没能在规定的时间内完成,主要原因是我花了很多时间去看了论文之外的相关资料,以下是这次assignment遇到的几个问题:
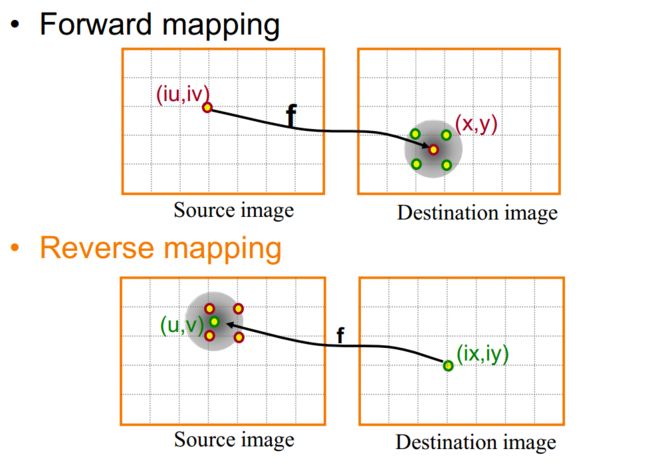
1、Forward Mapping ? Reverse Mapping ?
一开始读文章的时候,我对warping还不是太了解。两篇论文都是在讲述如何将坐标算出来,看完论文,我觉得好像是在说Forward Mapping,这也算是我对warping问题的初步理解。于是我上网找了一些相关资料,发现还有Reverse Mapping这种方式,同时也了解了两种方式的不同。原来大多数方法用的是Reverse Mapping,这个答案是正确的吗?论文里面并没有介绍这方面。这个问题我一开搞错了,导致了后面做得不对,后来才知道,原来文章中使用的是Forward Mapping。不过,我这也算是给自己科普了:
其实,现在的方法很多基于Reverse mapping,通过映射函数算出来的坐标点可能并不是整数值,而这种情况的话,就会产生权重问题,而Reverse mapping的话则是通过周围点算出中间非整数坐标点的像素值进行拷贝的,所以更加合理,而且不易产生空白或者许多的白点。
Thinking:能不能把这次的任务中的两个方法用Reverse mapping做出来?
2、Memory leaks!
这个问题是最折腾人的,内存泄漏的问题,我弄了比较长的时间,甚至还在论坛上发帖求助,但是,未果。经过这次,总结出来这么几点:
No.1--delete []pointer和delete pointer,不要搞错啊!
No.2--delete前要记得判断非空
No.3--还有虚构函数记得要delete指针成员
No.4--delete之后的指针,如果还需要用到的话,记得令其等于NULL
No.5--变量最好初始化,申请空间的时候,可以+1,这样子可以避免越界
No.6--delete和new不要忘记是成对出现的,申请空间之后,记得释放掉
总之,养成良好的习惯,可以降低内存泄漏这个错误出现的概率。
3、Radial Basis Function
使用RBF方法的话,需要解方程求出function对应的Ai,也就是系数,然后还要算出仿射分量Tx+B中矩阵T和向量B,总的来说,总共有2N+6个未知数,每一维有N+3个未知数。
通过N个控制点可以得到N个方程,但是,还不够求未知数,所以再需要三个方程。这个方程就是仿射可微条件:
所有Ai相加只和为0,Ai和Xi相乘只和为0,Ai和Yi相乘只和为0。
这样子就可以解出未知数
4、封装和继承
这次记得封装,但是忘了继承。写OOD的代码,最好是提取共性,封装,使用继承
这次的任务快做好了,才想起来可以使用继承,但是,好像有太急于提交,所以作罢,不过后来修改版就加入了继承。
虽然花了蛮多时间的,但是,这次收获很多!效率还是需要提高!加油!