【DP算法篇之初学】LIS\LCS\二维DP\带条件DP

最近参加2016华为软件精英挑战赛，题目也比较直接，就是求过定点的最短路。这题和以前练得不一样，感觉是不是要用DP(动态规划)。可是对于DP算法，我还是啥都不懂，于是好好补补。

主要是参考这篇博文：http://www.hawstein.com/posts/dp-novice-to-advanced.html（动态规划：从新手到专家）

看完入门，有点感觉了，然后是LIS问题，文中又提到了LCS问题，说这个更基础，于是转去看LCS。

关于LCS，有一篇清晰易懂的好博，见：http://songlee24.github.io/2014/11/27/dynamic-programming/（神奕的博客）

这张图是算法关键：

注意这里的C[i][j]，x[i],y[j]下标含义一样，指向相同的位置～

看完LCS，就拿poj1458练练手：

//time:16MS
//mem:396K

#include <string>
#include <iostream>
#include <vector>

using namespace std;

inline int max(int a, int b)
{
	return a > b ? a : b;
}

int LCS(const string x, const string y)
{
	int m, n, i, j;
	m = x.length();
	n = y.length();

	vector<vector<int> > table(m + 1, vector<int>(n + 1));
	
	for(i = 0; i < m + 1; ++i)
	{
		for(j = 0; j < n + 1; ++j)
		{
			if(i == 0 || j == 0)
				table[i][j] = 0;
			else if(x[i - 1] == y[j - 1])
				table[i][j] = table[i - 1][j - 1] + 1;
			else
				table[i][j] = max(table[i - 1][j], table[i][j - 1]);
		}
	}
	
	return table[m][n];
}

int main()
{
	string x, y;
	while(cin >> x)
	{
		cin >> y;
		cout << LCS(x, y) << endl;
	}
	return 0;
}

代码里特别要注意的是 table[][] 数组下标与 x[] ， y[] 下标含义不同，比如 x[i] 表示第 i+1 个元素，而 table[i][j]则表示截止到x[i-1]与y[j-1]的LCS。有关LCS序列的输出可以参照上面神奕的博客。

接着返回我们的 LIS问题：

最关键的状态转移方程如下：

设 A[i] 是该序列，并用 D[i] 表示以A[i]结尾的最长非降子序列的长度：
D[j] = max {1, A[i] + 1}，if A[j] >= A[i]，其中 i < j

此时，我们可以拿 leetcode #300 Longest Increasing Subsequence 练练手：

//leetcode300 Longest Increasing Subsequence
//144ms
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int i, j, len = 1, SIZE = nums.size();

	if(!nums.size())	//防止数组为空
		return 0;

	vector<int> D(SIZE, 1);

	for(i = 1; i < SIZE; ++i)
	{
		for(j = 0; j <= i - 1; ++j)
		{
			if(nums[j] < nums[i] && D[j] + 1 > D[i]) //递增序列，若求非降子序列，改nums[j] <= nums[i]
				D[i] = D[j] + 1;

			if(len < D[i])
			len = D[i];
		}
	}

	return len;
    }
};

此O(n^2)算法果然慢些，换成O(nlogn)：

//leetcode300 Longest Increasing Subsequence
//4 ms
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int i, j, maxLen = 1, SIZE = nums.size();
		
		if(!nums.size())
		    return 0;
		
		vector<int> D(SIZE, 1);
		D[1] = nums[0];
		D[0] = 0;	//此处设置要让D[0]小于数组里的所有值，此处的0感觉还是大了，不过居然过了。。巧合吧	
		for(i = 1; i < SIZE; ++i){
		    if(nums[i] > D[maxLen])
		        D[++maxLen] = nums[i];
		    else
		        for(j = maxLen; j >= 1; --j){
		            if(D[j] >= nums[i] && D[j-1] < nums[i]){  //找到数组D里第一个刚好小于nums[i]的值，替换之
		                D[j] = nums[i];
		                break;
		            }	    
		        }            
		}
		
		return maxLen;
    }
};

注意在该题中，子序列是递增的，而非非降子序列，所以与我们上面的公式稍微有所不同。我们还要注意里面的下标，还是依据C里面下标从0开始这一规则。

接着是二维DP问题，突然回想起LCS不就是个二维DP解法吗。。

可以用 leetcode 上 Unique Path I & II练手：

//Unique Path I
//0 ms
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int> > D(m, vector<int>(n));
        int i, j;
        
        if((m && n) == 0)	//防止原矩阵为空
            return 0;
        
        for(i = 0; i < m; ++i)
            D[i][0] = 1;
        for(i = 0; i < n; ++i)
            D[0][i] = 1;
            
        for(i = 1; i < m; ++i)
            for(j = 1; j < n; ++j)
                D[i][j] = D[i - 1][j] + D[i][j - 1];
        
        return D[m-1][n-1];
    }
};

//Unique Path II
//4 ms
class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        
        if((m && n) == 0)
            return 0;
        
        int i, j;
        vector<vector<int> > D(m, vector<int>(n, 0));
        
        for(i = 0; i < m; ++i)
            if(!obstacleGrid[i][0])
                D[i][0] = 1;
            else
                break;
                
        for(i = 0; i < n; ++i)
            if(!obstacleGrid[0][i])
                D[0][i] = 1;
            else
                break;
            
        for(i = 1; i < m; ++i)
            for(j = 1; j < n; ++j)
                if(!obstacleGrid[i][j])
                    D[i][j] = D[i - 1][j] + D[i][j - 1];
        
        return D[m - 1][n - 1];
            
        }
};

然后是带有额外条件的DP问题：题解巧妙地使用数组下标，立刻让我们对问题的解清晰不少，这其实显示了解题者挖掘出了题目中的一些性质。

题目：

无向图G有N个结点，它的边上带有正的权重值。

你从结点1开始走，并且一开始的时候你身上带有M元钱。如果你经过结点i， 那么你就要花掉S[i]元(可以把这想象为收过路费)。如果你没有足够的钱， 就不能从那个结点经过。在这样的限制条件下，找到从结点1到结点N的最短路径。 或者输出该路径不存在。如果存在多条最短路径，那么输出花钱数量最少的那条。 限制：1<N<=100 ; 0<=M<=100 ; 对于每个i，0<=S[i]<=100；正如我们所看到的， 如果没有额外的限制条件(在结点处要收费，费用不足还不给过)，那么， 这个问题就和经典的迪杰斯特拉问题一样了(找到两结点间的最短路径)。 在经典的迪杰斯特拉问题中， 我们使用一个一维数组来保存从开始结点到每个结点的最短路径的长度， 即M[i]表示从开始结点到结点i的最短路径的长度。然而在这个问题中， 我们还要保存我们身上剩余多少钱这个信息。因此，很自然的， 我们将一维数组扩展为二维数组。

题解：

我们用M[i][j]表示从开始结点到结点i的最短路径长度， 且剩余j元。通过这种方式，我们将这个问题规约到原始的路径寻找问题。 在每一步中，对于已经找到的最短路径，我们找到它所能到达的下一个未标记状态(i,j)， 将它标记为已访问(之后不再访问这个结点)，并且在能到达这个结点的各个最短路径中， 找到加上当前边权重值后最小值对应的路径，即为该结点的最短路径。 (写起来真是绕，建议画个图就会明了很多)。不断重复上面的步骤， 直到所有的结点都访问到为止(这里的访问并不是要求我们要经过它， 比如有个结点收费很高，你没有足够的钱去经过它，但你已经访问过它) 最后Min[N-1][j]中的最小值即是问题的答案(如果有多个最小值， 即有多条最短路径，那么选择j最大的那条路径，即，使你剩余钱数最多的最短路径)。

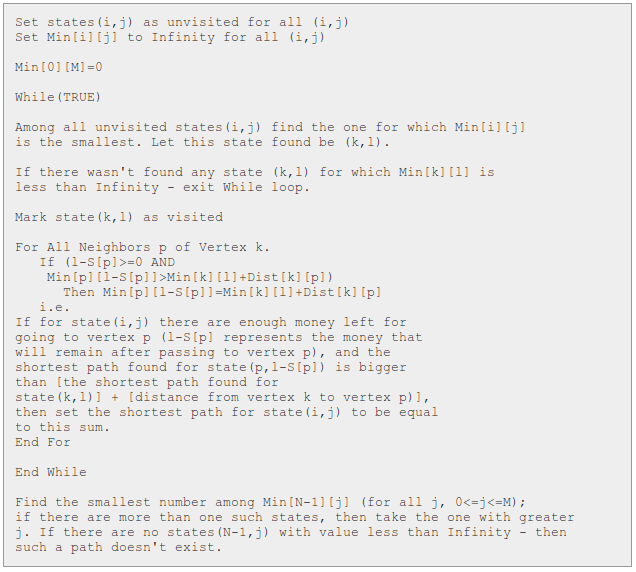
伪代码：

读着挺绕的，要试着走一遍过程，我花了好几个小时。。。其实过程和 Dijkstra 算法还是蛮相似的，在每一阶段的状态变化还是服从距离最短这一要点，同时保证钱的限制，所以增加了"剩余钱量"那一维度，所以为了能够在路径一样短时可以比较不同路径所所花的钱，我们把判断是否 visited 过的对象从点变成了 Min[][] 数组。注意到与 Dijkstra 算法的相同点与不同点即可。

不过，感觉此题的复杂度貌似不低。

最后是高级DP，它高在我们要仔细揣摩题目，将其规约为DP问题。

终于看完，收获很多。DP算法核心就在于将一个大问题的分成一个一个的阶段，即一个一个小问题（状态），然后试着解决它（状态转移方程）。状态与状态转移方程缺一不可。如果看起来是个DP问题，但你却无法定义出状态， 那么试着将问题规约到一个已知的DP问题。此外，我们还看出了DP算法与BFS，贪心算法的联系与区别。

马上会有面试，打算赶紧看看C++、TCP/IP知识，过段时间再用 leetcode 上的题练练手。习题可见：http://blog.csdn.net/u011095253/article/details/9262381（Leetcode上与DP有关的题目）