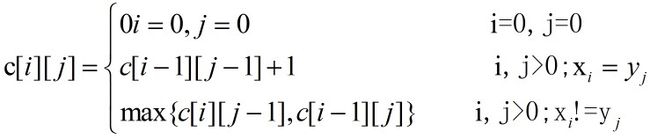【动态规划】最长公共子序列问题(LCS)

本文转载自：http://blog.csdn.net/liufeng_king/article/details/8500084

  问题描述：一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说，若给定序列X= { x1, x2,…, xm}，则另一序列Z= {z1, z2,…, zk}是X的子序列是指存在一个严格递增的下标序列 {i1, i2,…, ik}，使得对于所有j=1,2,…,k有 Xij=Zj。例如，序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列，相应的递增下标序列为{2,3,5,7}。给定两个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。例如，若X= { A, B, C, B, D, A, B}和Y= {B, D, C, A, B, A}，则序列{B,C,A}是X和Y的一个公共子序列，序列{B,C,B,A}也是X和Y的一个公共子序列。而且，后者是X和Y的一个最长公共子序列，因为X和Y没有长度大于4的公共子序列。给定两个序列X= {x1, x2, …, xm}和Y= {y1, y2, … , yn}，要求找出X和Y的一个最长公共子序列。

     问题解析：设X= { A, B, C, B, D, A, B},Y= {B, D, C, A, B, A}。求X，Y的最长公共子序列最容易想到的方法是穷举法。对X的多有子序列，检查它是否也是Y的子序列，从而确定它是否为X和Y的公共子序列。由集合的性质知，元素为m的集合共有2^m个不同子序列，因此，穷举法需要指数级别的运算时间。进一步分解问题特性，最长公共子序列问题实际上具有最优子结构性质。

      设序列X={x1,x2,……xm}和Y={y1,y2,……yn}的最长公共子序列为Z={z1,z2,……zk}。则有：

      (1)若xm=yn,则zk=xm=yn,且zk-1是Xm-1和Yn-1的最长公共子序列。

      (2)若xm!=yn且zk!=xm，则Z是Xm-1和Y的最长公共子序列。

      (3)若xm!=yn且zk!=yn，则Z是X和Yn-1的最长公共子序列。

      其中，Xm-1={x1,x2……xm-1}，Yn-1={y1,y2……yn-1},Zk-1={z1,z2……zk-1}。

     递推关系：用c[i][j]记录序列Xi和Yj的最长公共子序列的长度。其中，Xi={x1,x2……xi}，Yj={y1,y2……yj}。当i=0或j=0时，空序列是xi和yj的最长公共子序列。此时，c[i][j]=0；当i,j>0，xi=yj时，c[i][j]=c[i-1][j-1]+1；当i,j>0，xi!=yj时，

c[i][j]=max{c[i][j-1],c[i-1][j]}，由此建立递推关系如下：

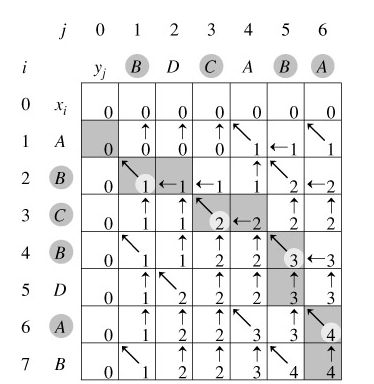
          构造最优解：由以上分析可知，要找出X={x1,x2,……xm}和Y={y1,y2,……yn}的最长公共子序列,可以按一下方式递归进行：当xm=yn时，找出xm-1和yn-1的最长公共子序列，然后在尾部加上xm(=yn)即可得X和Y的最长公共子序列。当Xm!=Yn时，必须解两个子问题，即找出Xm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者为X和Y的最长公共子序列。设数组b[i][j]记录c[i][j]的值由哪一个子问题的解得到的，从b[m][n]开始，依其值在数组b中搜索，当b[i][j]=1时，表示Xi和Yj的最长公共子序列是由Xi-1和Yj-1的最长公共子序列在尾部加上xi所得到的子序列。当b[i][j]=2时，表示Xi和Yj的最长公共子序列与Xi-1和Yj-1的最长公共子序列相同。当b[i][j]=3时，表示Xi和Yj的最长公共子序列与Xi和Yj-1的最长公共子序列相同。

     代码如下：

 //3d3-1 最长公共子序列问题
 #include "stdafx.h"
 #include <iostream>
 using namespace std;

 const int M = 7;
 const int N = 6;

 void output(char *s,int n);
 void LCSLength(int m,int n,char *x,char *y,int **c,int **b);
 void LCS(int i,int j,char *x,int **b);

 int main()
 {
     //X={A,B,C,B,D,A,B}
     //Y={B,D,C,A,B,A}
     char x[] = {' ','A','B','C','B','D','A','B'};
     char y[] = {' ','B','D','C','A','B','A'};

     int **c = new int *[M+1];
     int **b = new int *[M+1];
     for(int i=0;i<=M;i++)
     {
         c[i] = new int[N+1];
         b[i] = new int[N+1];
     }

     cout<<"序列X："<<endl;
     output(x,M);
     cout<<"序列Y："<<endl;
     output(y,N);

     LCSLength(M,N,x,y,c,b);

     cout<<"序列X、Y最长公共子序列长度为："<<c[M][N]<<endl;
     cout<<"序列X、Y最长公共子序列为："<<endl;
     LCS(M,N,x,b);
     cout<<endl;
 }

 void output(char *s,int n)
 {
     for(int i=1; i<=n; i++)
     {
         cout<<s[i]<<" ";
     }
     cout<<endl;
 }

 void LCSLength(int m,int n,char *x,char *y,int **c,int **b)
 {
     int i,j;

     for(i=1; i<=m; i++)
         c[i][0] = 0;
     for(i=1; i<=n; i++)
         c[0][i] = 0;

     for(i=1; i<=m; i++)
     {
         for(j=1; j<=n; j++)
         {
             if(x[i]==y[j])
             {
                 c[i][j]=c[i-1][j-1]+1;
                 b[i][j]=1;
             }
             else if(c[i-1][j]>=c[i][j-1])
             {
                 c[i][j]=c[i-1][j];
                 b[i][j]=2;
             }
             else
             {
                  c[i][j]=c[i][j-1];
                  b[i][j]=3;
             }
         }
     }
 }

 void LCS(int i,int j,char *x,int **b)
 {
     if(i==0 || j==0)
     {
         return;
     }
     if(b[i][j]==1)
     {
         LCS(i-1,j-1,x,b);
         cout<<x[i]<<" ";
     }
     else if(b[i][j]==2)
     {
         LCS(i-1,j,x,b);
     }
     else
     {
         LCS(i,j-1,x,b);
     }
 }

            LCSLength函数在计算最优值时，分别迭代X，Y构造数组b,c。设数组每个元素单元计算耗费时间O(1)，则易得算法LCSLength的时间复杂度为O(mn)。在算法LCS中，依据数组b的值回溯构造最优解，每一次递归调用使i，或j减小1。从而算法的计算时间为O(m+n)。LCS的回溯构造最优解过程如下图所示:

 

           算法的改进：对于一个具体问题，按照一般的算法设计策略设计出的算法，往往在算法的时间和空间需求上还可以改进。这种改进，通常是利用具体问题的一些特殊性。例如，在算法LCS_length和LCS中，可进一步将数组b省去。事实上，数组元素c[i,j]的值仅由c[i-1][j-1]，c[i-1][j]和c[i][j-1]三个值之一确定，而数组元素b[i][j]也只是用来指示c[i][j]究竟由哪个值确定。因此，在算法LCS中，我们可以不借助于数组b而借助于数组c本身临时判断c[i][j]的值是由c[i-1][j-1]，c[i-1][j]和c[i][j-1]中哪一个数值元素所确定，代价是Ο(1)时间。既然b对于算法LCS不是必要的，那么算法LCS_length便不必保存它。这一来，可节省θ(mn)的空间，而LCS_length和LCS所需要的时间分别仍然是Ο(mn)和Ο(m+n)。另外，如果只需要计算最长公共子序列的长度，则算法的空间需求还可大大减少。事实上，在计算c[i][j]时，只用到数组c的第i行和第i-1行。因此，只要用2行的数组空间就可以计算出最长公共子序列的长度。更进一步的分析还可将空间需求减至min(m, n)。

 //3d3-2 最长公共子序列问题
 #include "stdafx.h"
 #include <iostream>
 using namespace std;

 const int M = 7;
 const int N = 6;

 void output(char *s,int n);
 void LCSLength(int m,int n,char *x,char *y,int **c);
 void LCS(int i,int j,char *x,int **c);

 int main()
 {
     //X={A,B,C,B,D,A,B}
     //Y={B,D,C,A,B,A}
     char x[] = {' ','A','B','C','B','D','A','B'};
     char y[] = {' ','B','D','C','A','B','A'};

     int **c = new int *[M+1];
     for(int i=0;i<=M;i++)
     {
         c[i] = new int[N+1];
     }

     cout<<"序列X："<<endl;
     output(x,M);
     cout<<"序列Y："<<endl;
     output(y,N);

     LCSLength(M,N,x,y,c);

     cout<<"序列X、Y最长公共子序列长度为："<<c[M][N]<<endl;
     cout<<"序列X、Y最长公共子序列为："<<endl;
     LCS(M,N,x,c);
     cout<<endl;
 }

 void output(char *s,int n)
 {
     for(int i=1; i<=n; i++)
     {
         cout<<s[i]<<" ";
     }
     cout<<endl;
 }

 void LCSLength(int m,int n,char *x,char *y,int **c)
 {
     int i,j;

     for(i=1; i<=m; i++)
         c[i][0] = 0;
     for(i=1; i<=n; i++)
         c[0][i] = 0;

     for(i=1; i<=m; i++)
     {
         for(j=1; j<=n; j++)
         {
             if(x[i]==y[j])
             {
                 c[i][j]=c[i-1][j-1]+1;
             }
             else if(c[i-1][j]>=c[i][j-1])
             {
                 c[i][j]=c[i-1][j];
             }
             else
             {
                  c[i][j]=c[i][j-1];
             }
         }
     }
 }

 void LCS(int i,int j,char *x,int **c)
 {
     if(i==0 || j==0)
     {
         return;
     }
     if(c[i][j]==c[i-1][j-1]+1)
     {
         LCS(i-1,j-1,x,c);
         cout<<x[i]<<" ";
     }
     else if(c[i-1][j]>=c[i][j-1])
     {
         LCS(i-1,j,x,c);
     }
     else
     {
         LCS(i,j-1,x,c);
     }
 }

         运行结果如下：