hihocoder-1048 状态压缩·二(状压DP)
状态压缩·二:http://hihocoder.com/problemset/problem/1048
- 样例输入
-
2 4
- 样例输出
-
5
描述
历经千辛万苦,小Hi和小Ho终于到达了举办美食节的城市!虽然人山人海,但小Hi和小Ho仍然抑制不住兴奋之情,他们放下行李便投入到了美食节的活动当中。美食节的各个摊位上各自有着非常多的有意思的小游戏,其中一个便是这样子的:
小Hi和小Ho领到了一个大小为N*M的长方形盘子,他们可以用这个盒子来装一些大小为2*1的蛋糕。但是根据要求,他们一定要将这个盘子装的满满的,一点缝隙也不能留下来,才能够将这些蛋糕带走。
这么简单的问题自然难不倒小Hi和小Ho,于是他们很快的就拿着蛋糕离开了~
但小Ho却不只满足于此,于是他提出了一个问题——他们有多少种方案来装满这个N*M的盘子呢?
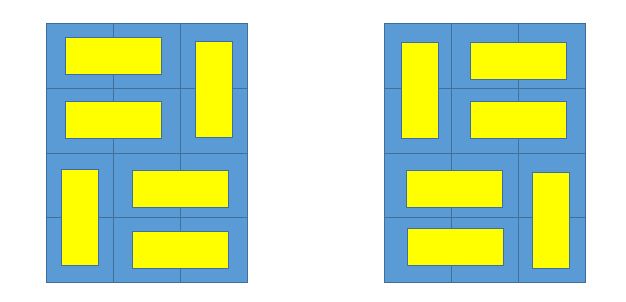
值得注意的是,这个长方形盘子的上下左右是有区别的,如在N=4, M=3的时候,下面的两种方案被视为不同的两种方案哦!
输入
每个测试点(输入文件)有且仅有一组测试数据。
每组测试数据的第一行为两个正整数N、M,表示小Hi和小Ho拿到的盘子的大小。
对于100%的数据,满足2<=N<=1000, 3<=m<=5。<>
输出
考虑到总的方案数可能非常大,只需要输出方案数除以1000000007的余数。
官方提示:我们来玩拼图吧!不过不同的枚举方式会导致不同的结果哦!
小Ho的观察力一向不错,这不,他很快便发现了M的取值范围只可能为3、4、5三种情况,但是这一发现并没有能够给他减轻多少烦恼。
虽然在过去一段时间的训练下,小Ho很快就意识到这道题目可能仍然是需要使用动态规划进行解决,但是他苦思冥想也没有能够想到很好的状态定义方式:“如果我每次枚举一块蛋糕的放置位置,那么我就需要存储下整个盘子的放置情况——也就是说2的(N*M)次方种状态,存不下呀存不下!”
小Hi看着小Ho憋闷的样子,也是知道他想错了方向,于是道:“你先别急,让我们从头来看看这个问题,首先你先告诉我,我们的问题是甚么?”
小Ho摇了摇头,想了想,道:“有多少种方案可以用1*2的正方形填满一个N*M的长方形?”
小Hi笑道:“是的,我们不妨称这个答案为sum(N, M),那么我们接下来要做的事情是不是要想办法把这个问题分解成若干子问题呢?”
小Ho道:“是的,我之前也是想到这里,我首先枚举一块蛋糕的放置位置,那么剩下的空闲位置有多少种方案被填满就是一个子问题了!由于这个位置的数量是在一直减少的,所以我可以按照一定的顺序依次求解出所有这样的问题的答案,但是这样的问题的数量太多了,根本计算不过来。”
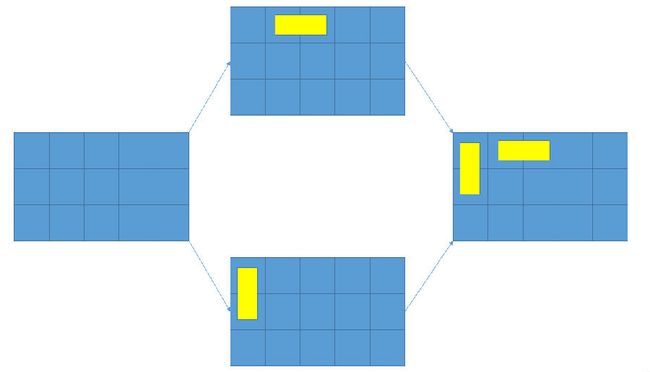
小Hi道:“你可是想的太简单了呢,真的只有算不过来的问题么?你且看这两种情况,虽然我第一次枚举的位置不同,但是只要第二次枚举的是另一种情况的第一次枚举,那么最终都会到达同样的状态,那么接下来是不是就会出现重复的统计啊?”
小Ho惊道:“是这样!那……那我应该怎么办呢?”
小Hi笑道:“我有一计,可解上述两大难题!”
小Ho道:“快快道来!”
小Hi挥挥手,表示不要着急,接着说:“你看!对于这样一种方案,按照你之前的方法,无论是1234的顺序枚举,还是4321的顺序枚举,最后统计到的都是这样一种方案,也就是无论是1~4的哪一种排列,都会是这样的方案,那么是不是说明,每一种方案都被统计了(N*M)!次?”
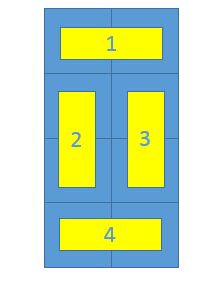
小Ho点了点头道:“是的!”想了想又接着说:“那么我是不是只要把最终答案都除以(N*M)!就能够得到正确的答案了呢?”
小Hi满脸无奈道:“真是个没志气的家伙,你为什么不干脆想办法使得每种方案都只被统计一次呢?”
小Ho:“怎么做?!教教我~”
小Hi道:”你想想,既然无论以什么样的排列顺序都会致使同样的结果,那么我们就想办法给它定义一个顺序便是了呢?比如说,对于每一块蛋糕,以其左(上)边一块的行号为第一关键字,列号为第二关键字的顺序,只有按照这个顺序递增的排列才是合法的!”
小Ho低头算了算,道:”是的!这样就只有1234这样一种顺序合法了,同样的,其他的每一种方案也都会只有一种对应的方案。但是我仍然不懂的是,我怎么保证在求解这个子问题的时候,一定能够只搜索出这样的方案呢?“
小Hi道:”这个简单!只要不是枚举每一块蛋糕放在什么地方?而是按照行号为第一关键字,列号为第二关键字的顺序,依次枚举每个位置上的蛋糕是如何放置的!通过这样的方式,来将一个问题分解成子问题!比如在下面的这个问题中,我当前要决定的便是黑色方块的蛋糕放置方案,而不同的放置方案——横放还是竖放,便会导出不同的子问题,并且这样是不会像之前的方法那样,有重复统计的。”
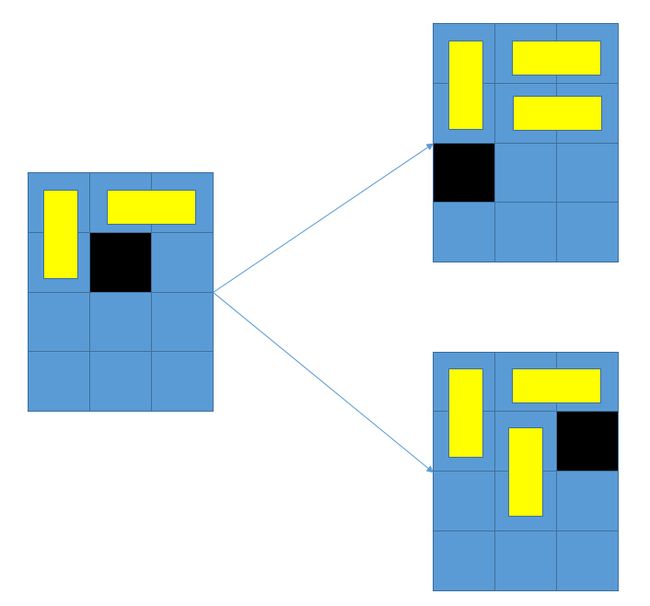
小Ho道:“原来是这样!仔细想想就会发现,这样导出的方案一定是符合我们之前的要求的,是合法的!但是不是说要解决两个问题么,现在我似乎还是要记录棋盘的局面呀,不然的话出现这种情况的时候,我是没有办法知道当前这个位置是否可以横放竖放,又是否已经在之前的放置中已经放置过了!”

小Hi忙道:“别急别急,你再想想到底要记录多少东西~”
“唔……其实好像只用记录两行就可以了!因为在枚举到(i, j)这个位置的时候,也就是当前枚举的位置所在的这一行,以及下一行。因为这之前的位置肯定都已经放置满了蛋糕,而这之后的位置肯定都还没有放置任何东西!”小Ho恍然大悟道。
“那你准备如何定义状态呢~”
“像这样,我令sum(i, j, p1, p2, ... , pM, q1, q2, ... , qM)表示:已经将第一行至第i-1行的盘子都已经填满了,当前正在尝试往(i, j)这个位置放置蛋糕,而第i行的放置情况用p1...pM表示,第i+1行的放置情况用q1...qM表示——0表示为空,1表示放置了蛋糕。那么sum(i, j, p1, p2, ... , pM, q1, q2, ... , qM)便表示在这种情况下,剩余的格子有多少种填充的方法,而我们要求的问题便是sum(1, 1, 0, 0, 0, ..., 0)了!”
小Hi笑道:“诶,你居然注意到了这个问题要求的是sum而不是best~这并不像之前的动态规划一样是求一个全局最优解,而是单纯的统计方案数!”
小Ho拍拍胸脯道:“你也不看看我是谁!而我觉得转移会是这样的……其中第一、二种情况是用于当前位置并不是空白位置时;第三种到第六种分别代表着当前位置的蛋糕摆放方向的2*2种可能。”
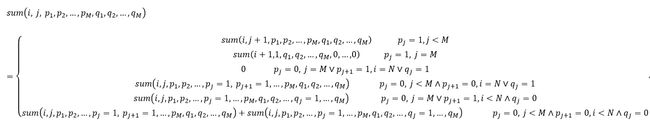
查看大图
小Hi点了点头,道:“没错!那你有没有觉得你这样的状态定义还是没有办法很好的根据M来进行转移?”
小Ho惊道:“是的呢!对了!我们还可以用上一周说的那种“状态压缩”的方式,将p1 ... pM, q1 ... qM 这2M个0/1表示成为一个整数,这样我的状态转移方程就会变成这样了!其中si表示s转换为2进制后从高到低第i位的值~”
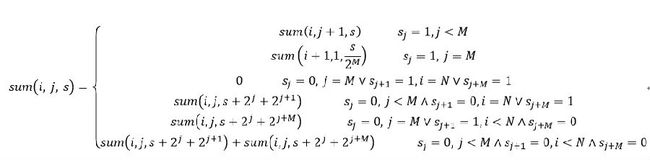
查看大图
“是的呢!”小Hi点了点头:“赶紧去写个程序算出来,我们就可以去吃蛋糕了!”
以前只做过2*n的棋盘用2*1的矩形覆盖,深切感觉到数据不同就真是不同的题;
n*m的感觉真的好难,看了提示,终于感觉能写了,不过还是调试了很久才AC
没怎么做过这种状压DP,想不到其他更简单的实现提示方法的代码
看到别的大神都是只压缩当前行的状态,还不能深刻理解,待以后能力更强了再学习!
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,m,mx,mxx,i,j,k,w[1005];
int dp[1005][1025];//按照提示,dp数组第二维存2行的状态,为了方便,1~m位存当前行的状态,m+1~2*m位存下一行的状态
int main() {
while(2==scanf("%d%d",&n,&m)) {
memset(dp,0,sizeof(dp));
mx=(1<<m)-1;
mxx=(1<<(m<<1));
dp[0][0]=1;
for(i=0;i<n;++i) {
for(k=0;k<m;++k)//题目已经说了行为第一关键字,列为第二关键字。刚开始枚举列和枚举状态写反了,导致某些与顺序有关的方案被重复计数
for(j=0;j<mxx;++j)
if(((1<<k)&j)==0) {//当第k+1位没有蛋糕时,可以放下蛋糕
if(k!=m-1&&((1<<(k+1))&j)==0)//当k+1不是m位的状态时,且第k+2位没有蛋糕时,表示蛋糕可以横放
dp[i][j|(1<<k)|(1<<(k+1))]=(dp[i][j|(1<<k)|(1<<(k+1))]+dp[i][j])%1000000007;
dp[i][j|(1<<(k+m))|(1<<k)]=(dp[i][j|(1<<(k+m))|(1<<k)]+dp[i][j])%1000000007;//当第k+1位没有蛋糕时,必定可以竖放
}
for(j=0;j<mxx;++j)//将第i行的状态转移至第i+1行
if((j&mx)==mx)//如果第i行已被蛋糕放满,则该状态可以转移至下一行
dp[i+1][j>>m]=dp[i][j];
}
printf("%d\n",dp[n-1][mx]);
}
return 0;
}