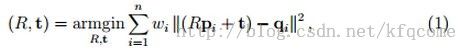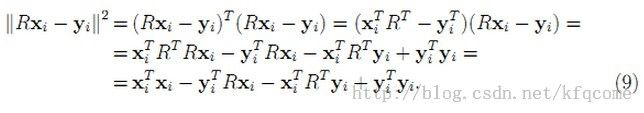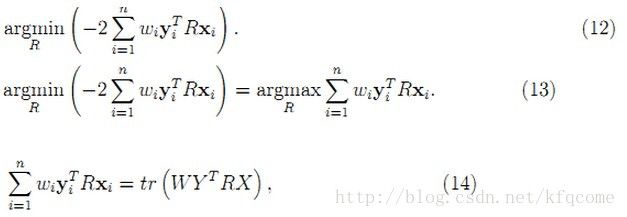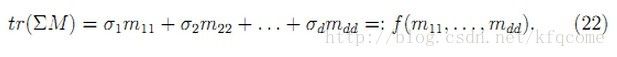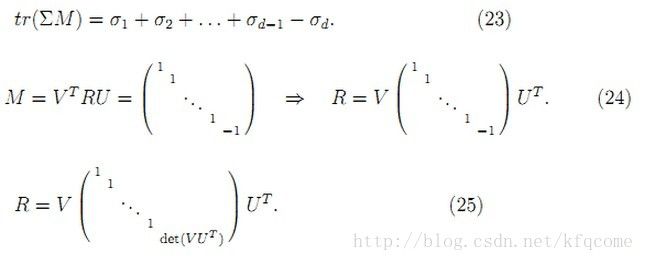使用SVD求最小二乘刚性转置

参见文章(Least-Squares Rigid Motion Using SVD)

一 问题描述

假设P={p1,p2,...,pn}和Q={q1,q2,...,qn}是两组Rd空间中的对应点集，现在想要根据这个两个点集的数据来计算出它们之间的刚性转置信息，可以知道这其实是一个最小二乘求优问题，问题可以用如下计算式描述：

其中wi>0，是点集中每个点对的权重。

要求(1)式中的最小值，即为求式中对R和t求导数为0的解。

二 计算位移

将(1)式中的R设为不变量对t进行求导，同时令F(t)=(R,t)，对F(t)求导可得：

从上可以看出，问题经过转化后变得更加简单，对原来的点集做一个减中心点的预处理，然后再求两个最小二乘的旋转量。

三 计算旋转量

将(8)式用矩阵表示形式展开，可得：

（由于旋转矩阵R是正交矩阵，因而有RRT = I）。同时可以知道上式中yiTRxi和xiTRTyi都是标量，而一个标量的转置仍然等于标量本身，因而有：

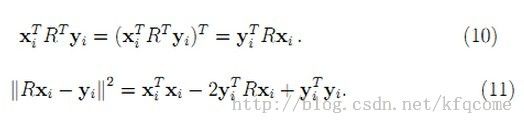
现在变成要求(11)式的最小值，而该式中只有一项与R有关，其他两项(xiTxi和yiTyi)都是常量，所以问题转换为求其中一项可变量的最小值，即

 

(14)式中的转换是将累加转换成矩阵相乘，其中W是n×n的对角矩阵，X和Y是3×n的矩阵，这些矩阵相乘后的迹就等于等式左边的值。同时，对于矩阵的迹，有如下变换关系：

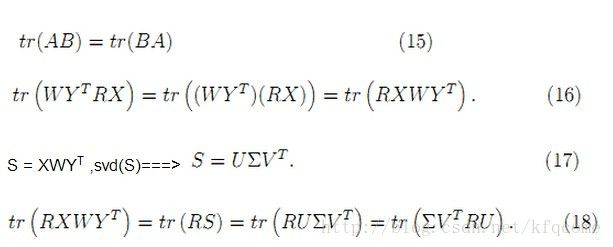
(18)式中最后一步的变换也用到了(15)式的性质。由于U、R、V都是正交矩阵，那么M=VTRU也是正交矩阵。

由上述两式可以知道，要求最大迹，就必须使得mii的值等于1，而M又是正交矩阵，那么M就必然是单位矩阵，即有

I = M = VTRU  => V = RU ⇒ R = VUT (21)

四 旋转结果校正

到上面(21)式为止，求得的R是最优的正交矩阵，但是这个正交矩阵既可以是旋转矩阵，也可以是反射矩阵。反射矩阵参见博文“旋转和反射”。

根据R的行列式值可以判断该结果是旋转矩阵还是反射矩阵，假如是反射矩阵，那么其行列式值就为-1。如果我们严格限定我们求解的必须是旋转矩阵，那么当前求解出来的反射矩阵就不符合要求。这个时候就必须求解下一个符合要求的最优解。

将目标问题重新组织成如下形式：

如果我们将mii当作变量，它的取值范围就是[-1,1]。函数f对于mii来说是线性的，所以它在定义域的边界上才取得极值。很显然对于所有的mii来说，所有都取1能取得最大的极值，但是该取值必须被排除（用这个得出的R是反射矩阵），那么下一个最优的(m11,m22,...,mdd)取值就是(1,1,...1,-1)，即除最后一个值取-1外，其他的值仍然为1。

为什么是取最后一个mdd为-1，这是进行SVD分解之后，Σ矩阵里对角线上的值经过了排序的，即σd的值最小。

五 使用范例

现在要对两个kinect摄像头进行空间位置标定，分别从两个kinect摄像头获取棋盘格角点的三维坐标，使用这两组点集即可计算出两个摄像头之间的刚性转置信息。

matlab代码如下:

clear;
clc;
PL0=[73.5716 -224.493 1781 25.9572 -191.805 1728 19.558 -189.427 1736 19.4678 -191.805 1728 19.558 -189.427 1736 19.558 -192.692 1736 16.1387 -168.168 1719 0 -232.847 1719 -13.0387 -231.884 1736 0 -177.042 1711;
-42.3757 -248.214 1736 -95.8748 -214.535 1702 -102.807 -212.45 1711 -102.807 -212.45 1711 -102.807 -212.45 1711 -103.288 -216.678 1719 -107.062 -182.989 1677 -126.631 -250.581 1686 -134.935 -251.078 1711 -124.754 -190.617 1661;
-158.289 -269.612 1686 -220.422 -236.623 1677 -223.571 -233.468 1677 -224.771 -237.893 1686 -227.936 -237.893 1686 -226.72 -236.623 1677 -226.579 -202.139 1653 -249.507 -265.614 1661 -253.843 -270.034 1669 -250.193 -207.35 1645;
-279.344 -292.324 1653 -347.628 -261.225 1653 -353.836 -258.116 1653 -353.836 -261.225 1653 -353.836 -258.116 1653 -353.836 -258.116 1653 -355.034 -220.792 1630 -383.011 -287.814 1645 -381.381 -292.753 1638 -377.656 -225.811 1622;
56.5635 -100.011 1772 6.48932 -65.0185 1728 6.48932 -65.0185 1728 6.51936 -65.3195 1736 3.2446 -65.0185 1728 3.21268 -64.3789 1711 6.39168 -41.6261 1702 -12.7833 -105.666 1702 -26.0773 -104.511 1736 -12.7232 -47.8044 1694;
-57.8291 -119.101 1711 -112.819 -84.778 1669 -117.134 -85.6415 1686 -117.134 -85.6415 1686 -117.69 -86.0479 1694 -119.658 -85.1843 1677 -110.724 -55.4689 1638 -137.89 -122.457 1669 -144.849 -123.044 1677 -135.907 -61.8955 1645;
-176.338 -141.974 1677 -235.89 -108.844 1653 -242.098 -105.734 1653 -240.926 -108.317 1645 -242.098 -105.734 1653 -242.098 -108.844 1653 -238.729 -73.5973 1630 -265.637 -139.265 1645 -266.929 -143.052 1653 -263.215 -79.7304 1630;
-296.525 -164.023 1645 -364.215 -131.862 1630 -367.276 -128.795 1630 -365.473 -131.215 1622 -365.473 -131.215 1622 -367.276 -131.862 1630 -358.522 -86.093 1578 -389.251 -154.188 1607 -392.268 -160.234 1607 -388.607 -92.8471 1592;
39.1161 29.3938 1736 -6.36164 60.5522 1694 -12.7833 64.0402 1702 -12.8509 61.1599 1711 -12.8509 61.1599 1711 -12.7833 60.8382 1702 0 84.3717 1661 -25.0709 21.9795 1669 -38.35 22.4141 1702 -25.0709 81.6381 1669;
-76.6998 6.40401 1702 -129.73 40.2321 1645 -134.11 40.6234 1661 -134.756 40.8191 1669 -134.756 40.8191 1669 -134.11 37.4985 1661 -123.026 70.877 1638 -147.631 6.16321 1638 -155.942 3.12487 1661 -147.631 67.7953 1638;
 -192.437 -12.4393 1653 -251.695 21.2683 1615 -258.355 21.5712 1638 -258.355 21.5712 1638 -255.831 21.3605 1622 -257.093 21.4659 1630 -242.132 56.9062 1592 -275.955 -9.11504 1615 -282.96 -15.4081 1638 -271.57 51.3958 1607;
-315.377 -33.4217 1615 -376.649 0 1592 -384.551 0 1600 -384.551 0 1600 -386.233 0 1607 -384.551 0 1600 -369.788 41.1671 1563 -403.553 -26.9556 1592 -406.542 -32.9457 1592 -401.18 35.4667 1571];

PR0=[  325.884 -278.142 1607 264.968 -216.657 1622 273.392 -219.738 1600 274.588 -220.7 1607 266.857 -215.722 1615 264.968 -216.657 1622 260.792 -191.415 1615 226.487 -251.458 1630 240.151 -246.865 1661 233.5 -188.377 1615;
209.969 -248.054 1669 162.221 -194.405 1694 163.849 -193.137 1711 166.183 -188.919 1702 163.849 -193.137 1711 160.636 -189.918 1711 147.292 -160.136 1669 120.052 -217.812 1728 134.339 -219.955 1745 131.029 -153.697 1702;
101.05 -225.352 1736 52.9658 -162.522 1763 60.1949 -167.532 1781 63.2181 -166.685 1772 59.8908 -166.685 1772 56.8508 -167.532 1781 39.5216 -125.394 1754 20.279 -186.251 1800 30.5707 -193.989 1809 26.8885 -127.967 1790;
-16.8992 -193.024 1800 -48.5796 -139.067 1848 -42.3156 -137.792 1878 -41.865 -139.82 1858 -41.865 -136.324 1858 -42.0903 -137.058 1868 -64.8948 -92.3973 1819 -81.5368 -156.285 1888 -81.1049 -158.991 1878 -75.5132 -89.4155 1828;
343.707 -139.53 1578 281.484 -86.093 1578 281.484 -83.1243 1578 281.484 -86.093 1578 281.484 -83.1243 1578 281.484 -86.093 1578 278.809 -58.8102 1563 244.413 -114.885 1607 257.76 -115.457 1615 258.924 -53.6742 1585;
230.794 -115.62 1661 173.814 -59.0867 1653 174.118 -53.9225 1686 176.338 -56.7896 1677 173.189 -53.6346 1677 177.284 -60.2663 1686 166.795 -24.7582 1645 138.147 -83.6925 1711 153.4 -86.4542 1702 150.425 -21.9795 1669;
116.807 -87.7749 1728 68.453 -32.6597 1736 72.4563 -32.9984 1754 72.8281 -33.1677 1763 72.4563 -32.9984 1754 69.1628 -32.9984 1754 61.3273 6.46798 1719 39.7244 -53.0684 1763 43.4741 -56.9608 1781 42.1804 9.75276 1728;
 0 -60.3115 1781 -30.5706 -10.21 1809 -34.6997 -3.47673 1848 -34.6997 -3.47673 1848 -34.6997 -3.47673 1848 -34.3242 -6.87811 1828 -46.8183 36.857 1781 -63.1354 -24.6002 1868 -66.2862 -31.4595 1858 -57.7446 40.8397 1809;
362.289 -5.85467 1556 296.671 49.5408 1549 298.012 52.6921 1556 298.012 49.7647 1556 298.012 49.7647 1556 298.012 49.7647 1556 294.181 75.1325 1536 269.632 17.8123 1578 286.657 15.1164 1607 277.56 79.0381 1556;
247.911 18.3993 1630 187.615 77.0402 1638 191.506 77.3694 1645 192.437 74.6358 1653 192.437 77.7457 1653 188.417 74.2746 1645 184.064 105.815 1607 162.18 49.998 1661 173.189 47.3247 1677 172.237 110.938 1638;
134.225 44.8281 1702 83.5308 99.7872 1711 83.9214 103.488 1719 84.3608 100.779 1728 83.9214 103.488 1719 84.3608 100.779 1728 75.5733 135.664 1677 58.674 78.3834 1736 58.9782 75.5069 1745 64.8929 146.292 1728;
23.1726 69.6522 1763 -23.7772 125.923 1809 -20.3805 129.326 1809 -20.3805 125.923 1809 -20.3805 129.326 1809 -23.5275 124.6 1790 -32.9347 168.292 1754 -40.7609 112.309 1809 -47.8172 106.086 1819 -37.1783 176.092 1800];

if ~all(size(PL0) == size(PR0))
    print 'size incorrect'
    return;
end

s0 = size(PL0);
numPoints = s0(1);

for i = 1:numPoints
    PL(i,:) = PL0(i,1:3);
    PR(i,:) = PR0(i,1:3);
end

%使用SVD求R
avgPL0 = sum(PL,1)/numPoints;
avgPR0 = sum(PR,1)/numPoints;
PLAvg = repmat(avgPL0,numPoints,1);
PRAvg = repmat(avgPR0,numPoints,1);

PL = PL - PLAvg;
PR = PR - PRAvg;

PL = PL'; %3*n
PR = PR'; %3*n

S0 = PL*PR';

[U, S, V] = svd(S0);
M = eye(3);
M(3,3) = det(V*U');

R = V*M*U';
T = avgPR0' - R*avgPL0';

PL = PL';
PR = PR';

%计算误差
sumErrors = 0;
for i = 1:numPoints
    pl = PL(i,:);
    pr = PR(i,:)';
    prr = R*pl' + T;
    diff = pr - prr;
    sumErrors = sumErrors + norm(diff);
end

sumErrors