算法导论滴2章图的基本算法--广度优先搜索

10、广度优先搜索，图的遍历 

1、  队列

（1）定义

队列也是一种运算受限的线性表。在这种线性表上，插入限定在表的某一端进行，删除限定在表的另一端进行。允许插入的一端称为队尾，允许删除的一端称为队头。

特点：队列中数据元素的入队和出队过程是按照“先进先出” 的原则进行的。因此，队列又称为“先进先出”的线性表，简称FIFO表。

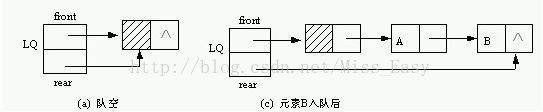
（2）实现－链队列

队列的链式存储结构简称为链队。它实际上是一个同时带有首指针和尾指针的单链表。头指针指向表头结点，而尾指针则指向队尾元素。从队尾插入，从队首删除。空的链队对列的判决条件是头指针和尾指针均指向头结点。

 

链队运算指针变化情况：

 

 

 

2、 广度优先搜索的算法思想

 

广度优先搜索遍历类似于树的按层次遍历。

    对于无向连通图，广度优先搜索是从图的某个顶点v0出发，在访问v0之后，依次搜索访问v0的各个未被访问过的邻接点w1，w2，…。然后顺序搜索访问w1的各未被访问过的邻接点，w2的各未被访问过的邻接点，…。即从v0开始，由近至远，按层次依次访问与v0有路径相通且路径长度分别为1，2，…的顶点，直至连通图中所有顶点都被访问一次。

 

广度优先搜索的顺序不是唯一的。

具体描述如下：

设图G的初态是所有顶点均未访问，在G 中任选一顶点i作为初始点，则广度优先搜索的基本思想是：

 

（1）从图中的某个顶点V出发，访问之；并将其访问标志置为已被访问，即visited[i]=1；

 

（2）依次访问顶点V的各个未被访问过的邻接 点，将V的全部邻接点都访问到；

 

（3）分别从这些邻接点出发，依次访问它们的未被访问过的邻接点，并使“先被访问的顶 点的邻接点”先于“后被访问的顶点的邻接点”被访问，直到图中所有已被访问过的顶 点的邻接点都被访问到。 

 

依此类推，直到图中所有顶点都被访问完为止 。

 

广度优先搜索在搜索访问一层时，需要记住已被访问的顶点，以便在访问下层顶点时，从已被访问的顶点出发搜索访问其邻接点。所以在广度优先搜索中需要设置一个队列Queue，使已被访问的顶点顺序由队尾进入队列。在搜索访问下层顶点时，先从队首取出一个已被访问的上层顶点，再从该顶点出发搜索访问它的各个邻接点。

 

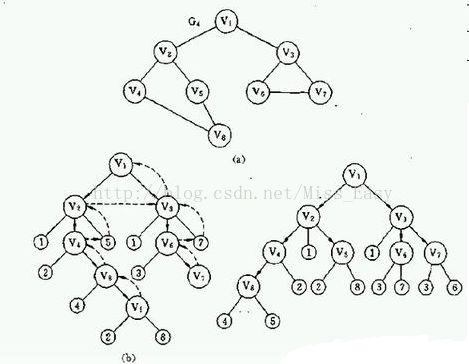
如下图（c）中为对图（a）的遍历：

按照广度优先算法，其遍历顺序为：

 

3、广度优先搜索算法的C语言描述

 

4、广度优先搜索算法的C++语言实现 

#include<iostream>
#define MAX_VERTEX_NUM 20
using namespace std;
typedef char VertexType;
//我们用邻接表来作图的存储结构
//表结点类型
typedef struct ArcNode{
int adjvex;
struct ArcNode *nextarc;
//int info;
}ArcNode;  

//邻接表结点
typedef struct VNode{
VertexType data;
ArcNode *firstarc;
}VNode,AdjList[MAX_VERTEX_NUM]; 

//图节点
typedef struct{
AdjList vertices;  
int vexnum,arcnum;
}ALGraph;

//链队结点的类型 
typedef struct Qnode{      
int data;
struct Qnode *next;
}Qnode,*QueuePtr; 

//链队指针类型 
typedef struct{ 
QueuePtr front;
QueuePtr rear;
}LinkQueue;

int visited[MAX_VERTEX_NUM]; 
//查找顶点对应的下标值
int LocateVex(ALGraph G,char u)
{
int i;
for (i=0;i<G.vexnum;i++)
{ 
if(u==G.vertices[i].data) 
return i; 
}
if (i==G.vexnum) 
{
cout<<"error!"<<endl;
exit(1);
}
return 0;
}
//初始化队列
void InitQueue(LinkQueue &Q)
{ 
Q.front=Q.rear=(QueuePtr)malloc(sizeof(Qnode));
if(!Q.front) 
exit(1); //存储分配失败
Q.front->next=NULL;
}
//进队
void EnQueue(LinkQueue &Q,int e)
{ 
QueuePtr p;
p=(QueuePtr)malloc(sizeof(Qnode)); 
p->data=e;
p->next=NULL;
Q.rear->next=p;
Q.rear=p;
}
//判断是否为空
int QueueEmpty(LinkQueue &Q)
{ 
return (Q.front==Q.rear? 1:0);
}
//删除队列元素
void DeQueue(LinkQueue &Q,int &e)
{ 
QueuePtr p;
if(QueueEmpty(Q))
{
cout<<"\n Queue is free!";
exit(1);
}//if
p=Q.front->next;
e=p->data;
Q.front->next=p->next;
if(Q.front->next==NULL)
Q.rear=Q.front; 
free(p);
} 


void CreateALGraph_adjlist(ALGraph &G)
{     
int i,j,k;  
char v1,v2;
ArcNode *p;//临接表节点
cout<<"Input 顶点数 & 边数:\n";//输入顶点8和边数10
cin>>G.vexnum;
cin>>G.arcnum;
cout<<"Input 各顶点(以空格隔开各个数据):\n"; 
for (i=0;i<G.vexnum;i++)
{     
cin>>G.vertices[i].data;//注意点，解说
G.vertices[i].firstarc=NULL;
}


//"r","s","t","u","v","w","x","y"
//{0,1},{0,4},{1,5},{2,3},{2,5},{2,6},{3,6},{3,7},{5,6},{6,7}
cout<<"Input 边(v1,v2)以回车分开各个数据:\n";
for (k=0;k<G.arcnum;k++)//建立邻接表
{
cin>>v1;
cin>>v2;
i=LocateVex(G,v1);
j=LocateVex(G,v2);
p=(ArcNode*)malloc(sizeof(ArcNode));
p->adjvex=j;   
p->nextarc=G.vertices[i].firstarc; //前插法,即每次都插入到头结点的后面
G.vertices[i].firstarc=p;
cout<<"Next:\n";
}     
return;
}


void BFSTraverse(ALGraph &G)
{
LinkQueue Q; 
for(int v=0;v<G.vexnum;++v) //之所有节点都未访问
visited[v]=false;
InitQueue(Q);//初始化队列
cout<<"广度遍历结果"<<endl;
for(int v=0;v<G.vexnum;++v)
if(!visited[v])//未被访问的
{
EnQueue(Q,v);//未被访问的进队
while(!QueueEmpty(Q))//队列非空
{
int u;       
DeQueue(Q,u);//u=队列最早进队的元素
visited[u]=true;//将u置为已被访问
cout<<G.vertices[u].data<<" ";//visit一下，输出节点元素
for(ArcNode *w=G.vertices[u].firstarc;w;w=w->nextarc)//访问节点的邻接表
if(!visited[w->adjvex])
EnQueue(Q,w->adjvex);
}
}
cout<<endl;
}

int main()
{
ALGraph G;
CreateALGraph_adjlist(G);
cout<<endl;
BFSTraverse(G);
system("pause");
}

结果如下图：

5、  广度优先搜索和深度优先搜索

 

深度优先搜索算法涉及的是堆栈，广度优先搜索涉及的是队列。