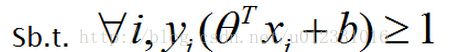SVM-SVC学习心得
SVM是Support Vector Machines（支持向量机）的缩写，可以用来做分类和回归。SVC是SVM的一种Type，是用来的做分类的，SVR是SVM的另一种Type，是用来的做回归的。
接受老师的批评，首先介绍一下SVM的核心算法。
（一）最大分类间距
上图的那些分类线中，到底哪个是最优的呢？从直观上而言，这个分类线应该是最适合分开两类数据的直线。而判定“最适合”的标准：离这条直线距离最近的的点的距离间隔最近。SVM就是寻找这样一条分类边界（超平面）。因为以下的示例图都是以二维为例，所以我就没有引入超平面，而用分类边界的概念。
支持向量：支持向量就是离分类边界最近的点。如上图所示用绿色圆圈圈起来的就是支持向量，它决定分类边界。SVM的准则就是最大化这个Margin. Margin是支持向量的间距，如上图所示。怎么最大化这个间距呢，下面介绍一下：
点x+和x- 是支持向量，分别代表正例和负例。求M的大小，就是求红色线和棕色线的距离。求两条直线的距离等价于求一条线上的点（如x-）到另一条直线的距离。即求（x-,-1）点到直线theta'*(x+)=1的距离M=2/||theta||;最大化M等价于最小化||theta||(向量的二范数)
那现在分类问题就变成一个二次最优化问题了：
Sb.t即为约束条件。这里详细介绍一下这个约束条件，很多资料还有博客都有很专业详细的介绍这一块点击，我们就朴素的描述一下这个约束条件。
记f(xi)=theta'*(xi)+b
在棕色线右边的数据点f(xi)>=1;且因为这些点的label(标签)yi为1，所以若正确分类，必然要求yi*f(xi)>=1；
同理，对红色线左边的点若正确分类，必然要求yi*f(xi)>=1；
对任意一点进行约束，就可以得到上图中的约束条件：
这个约束条件的意思就是要求每一点都正确分类。
但是若出现一下情况，用这个约束条件得到的分类边界就不是很好
图中用黑色圈起来的蓝点，若是再往右偏一些，可能就不能寻找到分类边界了。这种异常值的出现，要求我们修改一下约束条件，适当放宽一下约束条件。即允许一定比例的错分。因此便引入松弛变量
称为松弛变量(slack variable) ，表示对应点xi允许出现的分类误差。当然，如果任意大的话，那任意的分类边界（超平面）都是符合条件的了。所以，我们在原来的目标函数后面加上一项，使得这些的总和也要最小。现在优化问题就变成上图所示公式。（注意，这里约束条件也变了，没有以前的约束强了）
上图黑色的虚线是不加松弛变量的分类结果。粉色的是加了的分类结果，分类间距增加了。
参数C是一个常数，它是在最大分类间距和错分之间的一种折中，若C较大，这就要求较小，表示对错误的容忍就较小，分类间距相应就小一些。若C较小，这表示对错误的容忍就较大，分类间距相应就大一些。
至此，SVM的第一个核心内容最大间距原则，已经讲完，可以做线性分类器。