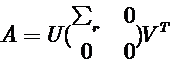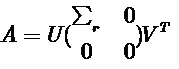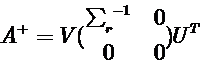超定方程 最小二乘解 奇异值分解(SVD)
1. 奇异值分解SVD
任意矩阵A (mxn)(这里仅考虑实数矩阵的情况), 都能被奇异值分解为:
其中, U是mxm的正交矩阵, V是nxn的正交矩阵, Σr是由r个沿对角线从大到小排列的奇异值(非负)组成的方阵. r就是矩阵A的秩.
V的列向量组成一套对A的正交“输入”或“分析”的基向量,这些向量是ATA的特征向量。
U的列向量组成一套对A的正交“输出”的基向量,这些向量是AAT的特征向量。
Σr对角线上的元素可视为在输入与输出间进行的纯量的"膨胀控制".这些是ATA和AAT的特征值的非零平方根.
ATA=VΣrTUT UΣrVT= V(ΣrTΣr)VT
AAT=UΣrVTVΣrTUT = U(ΣrΣrT)UT
2. Moore-Pseudo逆
任意矩阵A, 若存在矩阵X, 使得:
则称X是A的Moore-Pseudo逆, 简称广义逆, 记为A+.
矩阵A的广义逆是唯一的, 并且可以利用A的SVD分解进行计算. 令A的SVD分解为:
不难验证
当矩阵A满秩时,其M-P逆A+可以由表达式计算得到. 特殊地,当A列满秩(即ATA可逆)时,
这个特殊的伪逆构成一个左逆,即A+A = I. 当A行满秩(即AAT可逆)时,
这个特殊的伪逆构成一个右逆,即AA+ = I.
3. 线性最小二乘问题
考虑线性方程组Ax=b, 求其最小二乘解.
如果A的秩是n, 则其唯一解是A+b; 如果秩小于n, 则有无穷多解, 其中的最小范数解仍然是A+b. 我们通常关心的也就是这个解.
对于齐次线性方程组Ax=0。当A行数大于列数时,需要求解最小二乘解。在||x||=1的约束下,其最小二乘解为矩阵ATA最小特征值所对应的特征向量。求解方法有两种(matlab):
1) [V D] = eig(A'*A);D为A'*A的特征值对角矩阵,V为对应的特征向量。找到最小特征值对应的V中的特征向量即为最小二乘解。
2)使用SVD分解矩阵A,[U S V] = svd(A); U由A*A'的特征向量组成,V由A'*A的特征向量组成。因此,奇异值矩阵S中最小的奇异值对应的V中的奇异向量即为最小二乘解。
对于超定方程(非齐次线性方程组的一种)的最小二乘解的情况。Ax=b; 当A的行数大于列数时,方程组无解,需要求解最小二乘解。在matlab中使用一个左除命令就可以得到最小二乘意义下的解。matlab: A\b.