hdu1159 Common Subsequence

Common Subsequence


Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 29956    Accepted Submission(s): 13492




Problem Description
A subsequence of a given sequence is the given sequence with some elements (possible none) left out. Given a sequence X = <x1, x2, ..., xm> another sequence Z = <z1, z2, ..., zk> is a subsequence of X if there exists a strictly increasing sequence <i1, i2, ..., ik> of indices of X such that for all j = 1,2,...,k, xij = zj. For example, Z = <a, b, f, c> is a subsequence of X = <a, b, c, f, b, c> with index sequence <1, 2, 4, 6>. Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y. 
The program input is from a text file. Each data set in the file contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct. For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line. 
 


Sample Input
abcfbc abfcab
programming contest 
abcd mnp
 


Sample Output
4
2
0

dp经典，最长公共子序列

dp的核心是确定状态，找出子问题最优解，推出状态转移方程，然后求解

设d(i,j)为A1,A2,A3,...,Ai和B1,B2,B3,...,B j的最长公共子序列长度，则当A[i] = B[j]的时候，d(i, j) = d(i - 1, j - 1) + 1

否则d(i, j) = max{ d(i - 1, j), d(i, j - 1) }

d(i, j) = d(i - 1, j - 1) + 1是因为假如当前位置A[i] = B[j]也就是当前位置字符一样，就说明匹配，d(i, j)前一个状态是d(i - 1, j - 1)而不是d(i - 1, j)或d(i, j - 1)的原因是

如果是这两个，那么会出现同一个字符重复匹配的情况，显然是不合法的操作，若前一个状态是d(i - 1, j - 1)，其加一刚好两个字符串比对的长度自然加一。

对于d(i, j) = max{ d(i - 1, j), d(i, j - 1) }的理解是，若当前位不匹配，如匹配到abf 和 abcfb，是选3而不是2作为当前位最大公共子序列长度，匹配当前位置f 和 b不匹配，则必然这个匹配位置不会对匹配长度贡献一位，

当前的最长匹配长度肯定是ab abcfb的公共长度和abf  abcf公共长度中大的一个，因为当前位不匹配，相当于对结果没影响，即不会在上一个状态加一

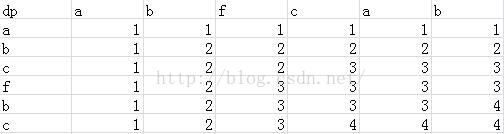
附上abcfbc abfcab的dp数组的最终图

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>

using namespace std;

char a[1005], b[1005];
int dp[1005][1005], lena, lenb;
int sizedp = sizeof(dp);

int main()
{
	while (~scanf("%s", a) && ~scanf("%s", b)) {
		lena = strlen(a);
		lenb = strlen(b);
		memset(dp, 0, sizedp);
		for (int i = 0; i < lena; i++) {  //A的任意长度和B的任意长度的子串挨个匹配一遍
			for (int j = 0; j < lenb; j++) {
				if (a[i] == b[j]) {
					if (i - 1 >= 0 && j - 1 >= 0) {   //防止越界
						dp[i][j] = dp[i - 1][j - 1] + 1;
					}
					else {
						dp[i][j] = 1;
					}
				}
				else {
					int tem = 0;
					if (i - 1 >= 0)	{
						tem = max(tem, dp[i - 1][j]);
					}
					if (j - 1 >= 0) {
						tem = max(tem, dp[i][j - 1]);
					}
					dp[i][j] = tem;
				}
			}
		}
		printf("%d\n", dp[lena - 1][lenb - 1]);
	}
	return 0;
}