Chapter3--Stacks and Queues
本章将回顾一下基本的栈和队列的数据结构,在此不再详细的介绍栈和队列的数据结构的理论,通过代码和例题在进一步学习。
首先,先把顺序栈,链栈,以及C++中的stack类模板通过代码简单的介绍。
顺序栈:
#include<iostream>
using namespace std;
const int MAXSIZE = 100;
typedef int ElemType;
//定义顺序栈的数据结构
typedef struct seqStack
{
//定义静态的数组
ElemType data[MAXSIZE];
int top;
}tSeqStack;
tSeqStack *s;
//入栈操作
void Push(ElemType e)
{
if(s->top==MAXSIZE-1)
{
return ;
}
(s->top)++;
s->data[s->top] = e;
}
//出栈操作
void Pop()
{
if(s->top == -1)
{
return ;
}
//cout<<s->data[s->top]<<endl;
(s->top)--;
}
//获取栈顶元素
ElemType Top()
{
return s->data[s->top];
}
//判断栈是否为空
bool Empty()
{
return s->top == -1;
}
int main()
{
int a[]={10,9,8,7,6,5,4,3,2,1};
int len = sizeof(a)/sizeof(a[0]);
s = new tSeqStack();
s->top = -1;
for(int i=0;i<len;i++)
Push(a[i]);
if(!Empty())
{
cout<<"the stack is not empty."<<endl;
}
cout<<"The top element is "<<Top()<<endl;
for(int i=0;i<len;i++)
Pop();
if(Empty())
{
cout<<"the stack is empty."<<endl;
}
system("pause") ;
return 0;
}
#include<iostream>
using namespace std;
typedef int ElemType ;
typedef struct StackNode
{
ElemType data;
struct StackNode *next;
}tStackNode;
tStackNode *top = NULL ;
static int cnt;
//创建栈
void createStack()
{
top = new StackNode();
cnt = 0;
top->next = NULL;
}
//入栈
void Push(ElemType e)
{
tStackNode *s = new tStackNode();
s->data = e;
s->next = top;
top = s;
cnt++;
}
//出栈
void Pop()
{
tStackNode *p = top;
top = p->next;
cnt--;
delete p;
}
//获取栈顶元素
ElemType Top()
{
return top->data;
}
//栈是否为空
bool Empty()
{
return cnt == 0 ;
}
int main()
{
int a[]={10,9,8,7,6,5,4,3,2,1};
createStack();
int len = sizeof(a)/sizeof(a[0]);
for(int i=0;i<len;i++)
Push(a[i]);
if(!Empty())
{
cout<<"the stack is not empty."<<endl;
}
cout<<"The top element is "<<Top()<<endl;
for(int i=0;i<len;i++)
{
cout<<Top()<<" ";
Pop();
}
if(Empty())
{
cout<<"\nthe stack is empty."<<endl;
}
system("pause");
return 0;
}
C++STLStack类模板:
#include<iostream>
#include<stack>
using namespace std;
int main()
{
stack<int> s;
s.push(7);
s.push(5);
s.push(3);
s.push(1);
cout<<"the size of stack is "<<s.size()<<endl;
if(!s.empty())
{
cout<<"the stack now is not empty."<<endl;
}
while(!s.empty())
{
cout<<s.top()<<endl;
s.pop();
}
cout<<"the size of stack is "<<s.size()<<endl;
if(s.empty())
{
cout<<"the stack now is empty."<<endl;
}
system("pause");
return 0;
}
结果:
3.1 Describe how you could use a single array to implement three stacks.
即:如何用一个数组来实现三个栈。这里我们只介绍一个实现起来很简单,但是效率并不是很高的方式。
算法分析:将数组等分成三个相等的部分,然后允许单独的栈在有限的空间内生长。(注意:"["代表包含,")"代表不包含)
>>对于栈1,我们将会使用[0,n/3)
>>对于栈2,我们将会使用[n/3,2n/3)
>>对于栈3,我们将会使用[2n/3,n)
这种方法是基于这种假设:对于单独的栈我们没有单独额外的使用信息。我们不能修改或者使用任何额外的空间。有了这些限制,我们可以选择等分这个数组。
#include<iostream>
using namespace std;
const int stack_size = 300;
int *buffer = new int [stack_size * 3];
int stack_pointer[] = {0,0,0};//stack poiter to track top elem
void push(int stack_num ,int value)
{
int pos = stack_num*stack_size + stack_pointer[stack_num] + 1;
buffer[pos] = value;
stack_pointer[stack_num]++;
}
int pop(int stack_num)
{
int pos = stack_num * stack_size + stack_pointer[stack_num];
stack_pointer[stack_num]--;
int value = buffer[pos];
buffer[pos] = 0;
return value;
}
int peek(int stack_num)
{
int pos = stack_num * stack_size + stack_pointer[stack_num];
return buffer[pos];
}
bool is_empty(int stack_num)
{
return stack_pointer[stack_num] == stack_num * stack_size;
}
int main()
{
for(int i=0;i<30;i++)
{
push(i/10,i);
}
cout<<peek(0)<<endl;
cout<<peek(1)<<endl;
cout<<peek(2)<<endl;
cout<<is_empty(0)<<" "<<is_empty(1)<<" "<<is_empty(2)<<endl;
for(int i=0;i<30;i++)
{
cout<<pop(i/10)<<" ";
if(i%10 == 9)
{
cout<<endl;
}
}
system("pause") ;
return 0;
}
3.2 How would you design a stack which, in addition to push and pop, also has a function min which returns the minimum element? Push, pop and min should all operate in O(1) time.
即:如何设计一个栈,除了入栈和出栈,还有一个取最小值的函数。入栈、出栈和取最小值都在O(1)的时间内完成。
算法一:You can implement this by having each node in the stack keep track of the minimum beneath itself. Then, to find the min, you just look at what the top element thinks is the min.
When you push an element onto the stack, the element is given the current minimum. It sets its “local min” to be the min.
代码:
#include<iostream>
#include<stack>
#include<algorithm>
#include<cstdlib>
using namespace std;
const int MAX_VALUE = 100000;
class NodeWithMin
{
public:
int value;
int min;
NodeWithMin(int v ,int m)
{
value = v;
min = m;
}
};
class StackWithMin : public stack<NodeWithMin>
{
private:
int newMin;
public:
void push(int value)
{
//newMin = min(value,min());
int minn = min();
value < minn ? newMin = value : newMin = minn;
stack<NodeWithMin> :: push( NodeWithMin(value,newMin) );
cout<<"value = "<<value<<" newMin = "<<newMin<<endl<<endl;
}
int min()
{
if( this->empty() )
{
cout<<"the stack is empty and return the max_value "<<MAX_VALUE<<endl;
return MAX_VALUE;
}
else
{
cout<<"top().value = "<<top().value<<" top().min = "<<top().min<<endl;
return top().min;
}
}
};
int main()
{
StackWithMin swm;
swm.push(2);
swm.push(3);
swm.push(1);
swm.push(6);
for(int i = 0;i<swm.size();i++)
{
cout<<swm.top().value<<endl;
swm.pop();
}
cout<<"the min value is = "<<swm.min()<<endl;
system("pause");
return 0;
}
算法二:算法一有一个问题:如果我们的栈足够大,那么我们就会浪费大量的空间去存储每一个栈中元素的最小值。如何改进?我们可以使用一个额外的栈来保存最小值。
代码:
#include<iostream>
#include<stack>
#include<algorithm>
#include<cstdlib>
using namespace std;
const int MAX_VALUE = 10000;
class StackWithMin2 : public stack<int>
{
private:
stack<int> *s2;
public:
StackWithMin2()
{
s2 = new stack<int>();
}
void push(int value)
{
if( value <= min() )
{
s2->push(value);
}
stack<int> :: push(value);
}
int pop()
{
int value = stack<int> :: top();
stack<int> :: pop();
if( value == min() )
{
s2->pop();
}
return value;
}
int min()
{
if( s2->empty() )
{
return MAX_VALUE;
}
else
{
return s2->top();
}
}
};
int main()
{
StackWithMin2 swm2;
cout<<swm2.min()<<endl;
swm2.push(10);
swm2.push(18);
swm2.push(6);
swm2.push(21);
swm2.push(6);
cout<<swm2.min()<<endl;
cout<<swm2.top()<<endl;
while( !swm2.empty() )
{
cout<<swm2.top()<<endl;
swm2.pop();
}
system("pause") ;
return 0;
}
3.3:Imagine a (literal) stack of plates. If the stack gets too high, it might topple. Therefore, in real life, we would likely start a new stack when the previous stack exceeds some threshold. Implement a data structure SetOfStacks that mimics this. SetOfStacks should be composed of several stacks, and should create a new stack once the previous one exceeds capacity. SetOfStacks.push() and SetOfStacks.pop() should behave identically to a single stack (that is, pop() should return the same values as it would if there were just a single stack).
即:想象一堆盘子,如果变得太高,那么它就可能倒塌。因此,当之前的栈要超出某个阈值的时候,我们可能新建一个新的栈。实现一个数据几个SetOfStacks来模仿这个。SetOfStacks应该由几个栈组成,当之前的栈超出容量时建立一个新栈。SetOfStacks.push()和SetOfStack.pop()应该独立的表现出一个单独的栈(也就是所,pop()应该返回相同的值好像它是一个单独的栈)
算法:
1.设定一个SetOfStacks类,设置每一个单独栈的容量capacity。
2.定义vector< stack<int> > stacks;vector容器中包含若干个栈。push或者pop都从最右面的那个vector元素(最右面的栈)开始操作。
代码:
#include<iostream>
#include<stack>
#include<cstring>
#include<cstdlib>
#include<vector>
using namespace std;
class SetOfStacks
{
private:
int capacity;
vector< stack<int> > stacks;
public:
SetOfStacks(int capacity)
{
this->capacity = capacity;
}
void push(int v)
{
if( stacks.size()!=0 && stacks[stacks.size()-1].size()!=capacity ) //add element to last stack
{
stacks[stacks.size()-1].push(v);
cout<<"the stack is not full, insert the value : "<<v<<endl;
}
else //create a new stack
{
stack<int> new_stack;
new_stack.push(v);
stacks.push_back(new_stack);
cout<<"create a new stack and insert the value : "<<v
<<" now the stacks size is "<<stacks.size()<<endl;
}
}
int pop()
{
int val = stacks[stacks.size()-1].top();
stacks[stacks.size()-1].pop();
if( stacks[stacks.size()-1].size()==0 ) stacks.pop_back();
return val;
}
bool empty()
{
return stacks.size() == 0;
}
};
int main()
{
SetOfStacks sos(7);
for(int i=0;i<19;i++)
{
sos.push(i);
}
for(int i=0;i<19;i++)
{
cout<<sos.pop()<<" ";
}
system("pause") ;
return 0;
}
运行:
3.4:In the classic problem of the Towers of Hanoi, you have 3 rods and N disks of different sizes which can slide onto any tower. The puzzle starts with disks sorted in ascending order of size from top to bottom (e.g., each disk sits on top of an even larger one). You have the following constraints:
(A) Only one disk can be moved at a time.
(B) A disk is slid off the top of one rod onto the next rod.
(C) A disk can only be placed on top of a larger disk.
Write a program to move the disks from the first rod to the last using Stacks.
无需过多解释,就是经典的汉诺塔问题:
代码:
#include<iostream>
#include<stack>
#include<cstdlib>
#include<cstring>
using namespace std;
class Tower
{
private:
stack<int> disks;
int index;
public:
Tower(int i)
{
//cout<<"the disks size is : "<<disks.size()<<endl;
index = i;
}
int get_index()
{
return index;
}
void add(int d)
{
if( !disks.empty() && disks.top()<=d )
{
cout<<"error placing disk "<<d<<endl;
}
else
{
//printf("push the disk %d into stack %d\n",d,get_index());
disks.push(d);
}
}
void move_top_to(Tower *t)
{
int top = disks.top();
disks.pop();
t->add(top);
cout<<"move disk "<<top<<" from "<<this->get_index()<<" to "<<t->get_index()<<endl;
}
void move_disks(int n , Tower *destination, Tower *buffer)
{
if( n > 0 )
{
move_disks(n-1,buffer,destination);
move_top_to(destination);
buffer->move_disks(n-1,destination,this);
}
}
void print()
{
while(!disks.empty())
{
cout<<disks.top()<<" ";
disks.pop();
}
cout<<endl<<endl;
}
};
int main()
{
Tower *tower[3];
for(int i=0;i<3;i++)
{
tower[i] = new Tower(i);
}
int n;
cout<<"please input the number of disks : ";
cin>>n;
for(int i=n;i>=1;i--)
{
tower[0]->add(i);
}
tower[0]->move_disks(n,tower[2],tower[1]);
cout<<"push all the tower 0 : ";
tower[0]->print();
cout<<"push all the tower 1 : ";
tower[1]->print();
cout<<"push all the tower 2 : ";
tower[2]->print();
system("pause") ;
return 0;
}
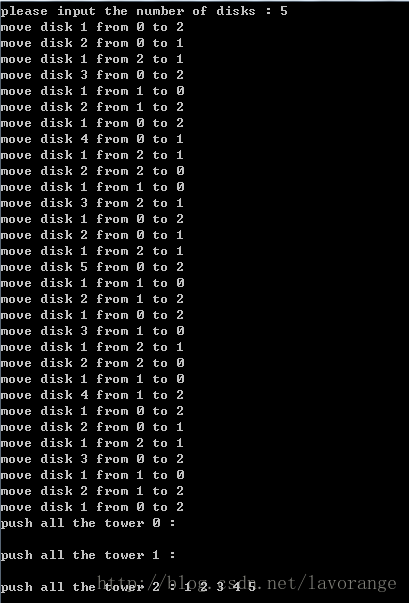
结果:
3.5:Implement a MyQueue class which implements a queue using two stacks.
即:使用两个栈来实现队列。
算法:栈和队列的主要区别就是顺序问题(队列:FIFO VS 栈:LIFO),我们需要按照逆序的方法来修改top()和pop()。我们需要第二个栈来逆序存储元素(通过将s1中的元素pop出来然后push到s2中去)。在s1的栈顶,有最新的元素,在s2的栈顶是最旧的元素。入队的时候,push到s1中,取栈顶或者出队的时候取s2的栈顶(s2非空)。当s2为空时,我们再按照逆序将s1中的元素转移到s2中去。
代码:
#include<iostream>
#include<stack>
#include<cstdlib>
#include<cstring>
#include<stdio.h>
using namespace std;
template<class T>
class MyQueue
{
private:
stack<T> s1,s2;
public:
int size()
{
s1.size() + s2.size();
}
void add(T value)
{
cout<<"push "<<value<<" into s1"<<endl;
s1.push(value);
}
T top()
{
if( !s2.empty() ) return s2.top();
while( !s1.empty() )
{
s2.push( s1.top() );
s1.pop();
}
return s2.top();
}
void dequeue()
{
if( !s2.empty() )
{
cout<<"pop "<<s2.top()<<" from s2"<<endl;
s2.pop();
return ;
}
while( !s1.empty() )
{
s2.push( s1.top() );
cout<<"push "<<s1.top()<<" from s1 to s2"<<endl;
s1.pop();
}
cout<<"pop "<<s2.top()<<" from s2"<<endl;
s2.pop();
return ;
}
};
int main()
{
MyQueue<int> mq1;
for(int i=0;i<5;i++)
{
mq1.add(i);
}
for(int i=0;i<3;i++)
{
mq1.dequeue();
}
mq1.add(5);
mq1.add(6);
mq1.dequeue();
mq1.dequeue();
mq1.dequeue();
mq1.dequeue();
cout<<endl;
MyQueue<string> mq2;
mq2.add("aaa");
mq2.add("bbb");
mq2.add("ccc");
mq2.dequeue();
mq2.dequeue();
mq2.dequeue();
system("pause");
return 0;
}
结果:
3.6:Write a program to sort a stack in ascending order. You should not make any assumptions about how the stack is implemented. The following are the only functions that should be used to write this program: push | pop | peek | isEmpty。
即:写一个程序来将一个栈排序。只能用几种方法:push|pop|top|empty.
算法:排序应该多用一个栈。这种方法就是将一个元素从原始栈中弹出,然后将它压入另外一个栈。如果压入新栈的元素违背了递增的顺序,我们将新栈中大于它的元素弹出放入原始栈中,然后压入新栈。算法的时间复杂度为O(n^2)。
代码:
#include<iostream>
#include<stack>
#include<cstring>
#include<cstdlib>
using namespace std;
stack<int> sort(stack<int> &s)
{
stack<int> buffer;
while(!s.empty())
{
int tmp = s.top();
s.pop();
cout<<"pop "<<tmp<<" from s"<<endl;
while( !buffer.empty() && buffer.top() > tmp )
{
s.push( buffer.top() );
cout<<"push "<<buffer.top()<<" from buffer back to s"<<endl;
buffer.pop();
}
buffer.push(tmp);
cout<<"push "<<tmp<<" into buffer"<<endl;
}
return buffer;
}
int main()
{
stack<int> s;
s.push(6);
s.push(1);
s.push(2);
s.push(5);
s.push(3);
s = sort(s);
while(!s.empty())
{
cout<<s.top()<<" ";
s.pop();
}
cout<<endl;
system("pause");
return 0;
}
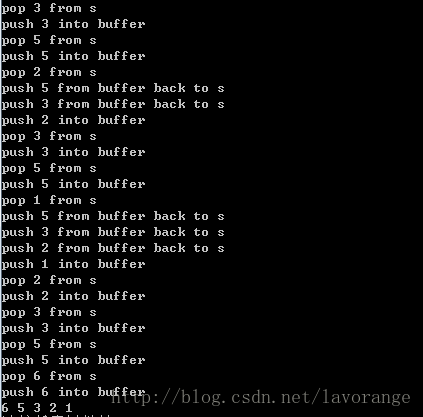
结果:
转载注明:http://blog.csdn.net/lavorange/article/details/16953243