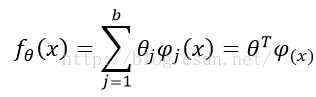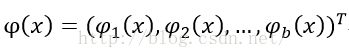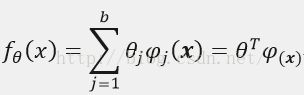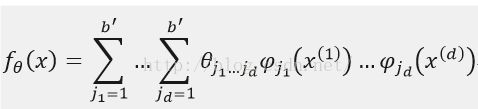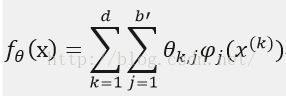机器学习模型——线性模型

     本文摘自《图解机器学习》一书，但是书上有些地方讲的比较繁琐，本文对其进行解释。

  对函数f 进行近似时，最简单的模型就是线性模型θXx，其中θ表示模型的参数（标量），说白了就是x的系数，我们要办的事情就是对这个参数进行学习，完成函数的近似计算。近似的好坏，就依赖于这个系数的选择。

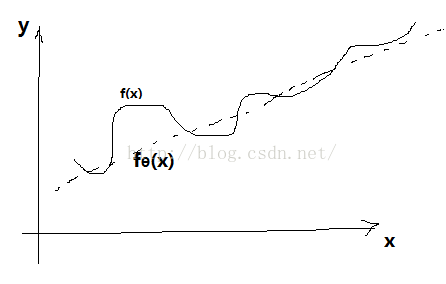
      线性模型对于参数θ而言是线性的，所以对数值的计算很简单易行。但是只能表现出线性的输入输入函数（即直线关系），所以在解决实际问题方面，往往没有太大的实用价值。从下图可以看出，线性模型与原非线性函数不能很好的近似。其中f(x)是原函数，fθ(x)是学习后的线性模型函数。

所以，为了使线性模型能够表示非线性的输入和输出，对上述的线性模型进行扩展，提出了基于参数的线性模型。

基于参数的线性模型表示方法为：

其中：

是基函数向量

是参数向量

虽然看着还是跟基于θ 的线性形式，但是把基函数变为多项式的形式，比如： 

         

或者

这样就能表示复杂的非线性模型了。

上述的一维的输入x的模型还适用于多维的向量形式，比如d为的向量形式

，b是基函数向量的个数。

使用一维的基函数构造多维基函数的方法有两种：乘法模型和加法模型。

乘法模型是指，把一维的基函数作为因子，通过使其相乘而获得多维基函数的方法。

b' 代表各维的参数个数。

由于乘法模型由多个不同的一维基函数任意组合而成，因此可以表示复杂函数。但是，所有参数的个数是，即总的输入维数是以d次方的形式呈指数级增长的。例如b'=10，d是100的时候，全部参数的个数将是10^100=1000...000(100个零)。这样的随着维数的增加，计算量呈指数级增长的现象，通常称为维数灾难。

  加法模型是指，把一维的基函数作为因子，通过使其相加而获得多维基函数的方法。

加法模型所有参数个数是b'd，只会随着输入维数d呈线性增长。例如b'=10，d=100的时候，全部参数的个数是10×100=1000.但是加法模型只考虑了一维基函数相加情况，表现的函数比较简单。

对比乘法模型和加法模型：

乘法模型表现力非常丰富，但是参数个数会随着输入维数d呈指数级增加。加法模型的参数个数是睡着输入维数d成线性增加。表现力相对较弱。

以上是对线性模型的一个概述，线性模型是一类统计模型的总称，包括：线性回归模型，方差分析模型，协方差分析模型，线性混合效应模型(或称为方差分量模型)。

在线性回归模型中，需要注意的是最小二乘法的相关应用：最小二乘估计，约束最小二乘估计，广义最小二乘估计，最小二乘估计统一理论。最小二乘估计的稳健性，两部估计，协方差改进法，多元线性模型。

在方差分析模型中，需要注意的是单向分类模型，两向分类模型，套分类模型，误差方差齐性及正态性检验。