“农田灌溉(Farm Irrigation), ZOJ2412”问题的一种解法

本博客是Pospro对“ZOJ2412，农田灌溉（Farm Irrigation）问题”的一种解答

题目描述：
Benny 有一大片农田需要灌溉。农田是一个长方形，被分割成许多小的正方形。每个正方形中都安装了水管。不同的正方形农田中可能安装了不同的水管。一共有11 种水管，分别用字母A～K 标明，如图(a)所示。


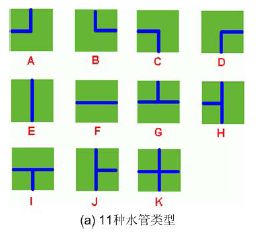
Benny 农田的地图是由描述每个正方形农田中水管类型的字母组成的矩阵。例如，如果农田的地图为：
ADC
FJK
IHE
则农田中水管分布如图(b)所示。

某些正方形农田的中心有水源，因此水可以沿着水管从一个正方形农田流向另一个正方形农田。如果水可以流经某个正方形农田，则整个正方形农田可以全部灌溉到。Benny 想知道至少需要多少个水源，以保证整个长方形农田都能被灌溉到？
例如，图(b)所示的农田至少需要3 个水源，图中的圆点表示每个水源。
输入描述：
输入文件中包含多个测试数据。每个测试数据的第1 行为两个整数M 和N，表示农田中有M行，每行有N 个正方形。接下来有M 行，每行有N 个字符。字符的取值为'A'～'K'，表示对应正方形农田中水管的类型。当M 或N 取负值时，表示输入文件结束；否则M 和N 的值为正数，且其取值范围是1≤M, N≤50。
输出描述：
对输入文件中的每个测试数据所描述的农田，输出占一行，为求得的所需水源数目的最小值。
样例输入： 
2 2
DK
HF
3 3
ADC
FJK
IHE
0 0
样例输出：
2
3

解题思路分析：

1. 问题是“至少”多少水源就能满足灌溉要求，所以很自然的，我们需要分析从某一点出发，水流最大可以到达的范围，所以需要用到深度优先搜索（DFS）。

2. 由于只要有一处来水就可以满足该地块的灌溉的要求，所以一旦在某次搜索中，该地块被搜索到，则本地块就可以置空，后续不需要再搜索此处。（同时，由于采用DFS，如果该地块存在多个来水/去水方向，各个来水方向的地块在本次搜索结束后，也一定会被置空）。

3.到达一个地块后，我们可以按照“上、右、下、左”的顺序分析此地块是否有水管通向相邻地块。本题的难点在于，如何判断相邻地块恰好有合适位置的水管把水引过去。Propos在这里采用的是位运算的方式来判断：

3.1即对于A～K这11中水管分布图

按照上、右、下、左的顺时针顺序，如果该方向有水路，则设置为1，无水路，则设为0，则有：
A＝1001＝9，   B＝1100＝12， C＝0011＝3，   D＝0110＝6
E＝1010＝10，  F＝0101＝5，   G＝1101＝13， H＝1011＝11

I＝0111＝7，     J＝1110＝14，  K＝1111＝15

3.2 相邻地块在对应点是否有水管接收来水，可以通过对应位置的0/1来判定：
向上引水：上面相邻地块必须在0010位置的水管
向右引水：右边相邻地块必须在0001位置的水管
向下....：   下面..............             1000..........

向左.... :     左边..............             0100..........

3.3 对应位是否是1可以通过位运算（&）来做

程序实现（分别对应于思路中的1，2，3）

1. DFS采用递归方式实现

2. 在DFS实现的开头，先保存该地块的水管分布，然后置零（因为0恰好表示与周围都无关联）

               currentField=field[i][j];    field[i][j]=0;

3.1 将水管分布用数字表示：
         pipeConfig[11]={9,12,3,6,10,5,13,11,7,14,15};
         实际样例输入的不是水管分布，而是A～K的字符，可以用下面语句加以转化：

                           field[i][j]=pipeConfig[field[i][j]-'A'];

3.2向上饮水（向上搜索）的语句如下：
         if( (currentField&'0x08')&&(i-1>=0)&&(field[i-1][j]&'0x02') )
                     DFS_Connect(i-1,j);

If中的第一部分currentField&'0x08'判断本地块是否存在向上的管路；

第二部分i-1>=0判断上面的地块是否存在（是否越界）；

第三部分field[i-1][j]&'0x02'判断上面地块是否有向下的水管引入来水。

思路分析得差不多了，下面是完整程序

/*
ZOJ2412，农田灌溉问题
2016.05.05 Mon Rain by Pospro
*/

#include <cstdio>
char field[51][51]; //地块最大覆盖范围
int m,n; //size of the field m行n列
unsigned char pipeConfig[11]={9,12,3,6,10,5,13,11,7,14,15};
//水管分布代码，详见博客http://blog.csdn.net/pospro


void DFS_Connect(int i, int j)
{
    char currentField=field[i][j]; //重置之前先保存当前地块的水管分布
    field[i][j]=0;

    //递归调用，分别向上、向右、向下、向左搜索
    //由于进入递归就将本地块置零（设成无通路状态），所以不会无限循环
     if( (currentField&'0x08')&&(i-1>=0)&&(field[i-1][j]&'0x02') )
        DFS_Connect(i-1,j);
     if( (currentField&'0x04')&&(j+1<n)&&(field[i][j+1]&'0x01') )
        DFS_Connect(i,j+1);
     if( (currentField&'0x02')&&(i+1<m)&&(field[i+1][j]&'0x08') )
        DFS_Connect(i+1,j);
     if( (currentField&'0x01')&&(j-1>=0)&&(field[i][j-1]&'0x04') )
        DFS_Connect(i,j-1);
}

int main()
{
    int i,j;
    int waterSource;
    while(1)
    {
        scanf("%d%d",&m,&n);
        if(m<=0||n<=0) break; //输入0，0时结束

        for(i=0;i<m;i++)
            scanf("%s",field[i]);

        waterSource=0; //新数据输入时，从新计数

        //接收输入，并转化为水管分布码
        for(i=0;i<m;i++)
        {
            for(j=0;j<n;j++)
            {
               field[i][j]=pipeConfig[field[i][j]-'A'];
               //将输入的字母转变成对应的水管分布码
            }
        }

        for(i=0;i<m;i++)
        {
            for(j=0;j<n;j++)
            {
                //已搜索过，已被连接至已有水源，故水源数不需要加1，直接跳过即可
                if(int(field[i][j])==0)
                    continue;
                else
                {
                    DFS_Connect(i,j);
                    waterSource++;
                }
            }
        }
        printf("%d\n", waterSource);
    }
    return 0;
}

输入范例：

2 2
DK
HF
3 3
ADC
FJK
IHE
0 0