DirectX 11游戏编程学习笔记之4: 第3章Transformations(变换)
本文由哈利_蜘蛛侠原创,转载请注明出处!有问题欢迎联系2024958085@qq.com
注:我给的电子版是700多页,而实体书是800多页,所以我在提到相关概念的时候,会使用章节号而非页码。同样的情况适合于“龙书”第二版。
上一期的地址:
DX 11游戏编程学习笔记之3
重点回顾:
===============================================================================
这一章还是比较重要的。当然,前两章也很重要;但是一方面前两章的内容比较简单,另一方面有些比较难的部分其实并不需要掌握,只需要大概知道就行了,所以其实它们跟这一章比起来显得不那么重要了。这一章的内容还是需要去仔细理解的;当然具体的公式你没有必要全部记住。
还是把这一章的学习目标放上来吧!
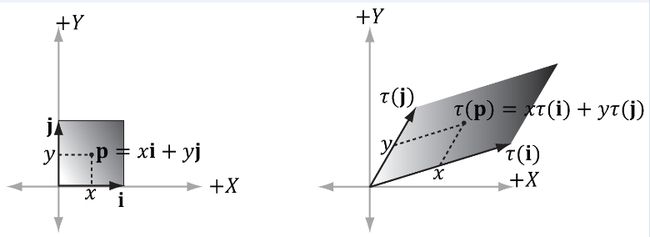
1、 To understand how linear and affine transformations can be represented by matrices.(理解为何线性变换和仿射变换可以由矩阵表示。)
2、 To learn the coordinate transformations for scaling, rotating, and translating geometry.(学会用来对几何体进行缩放、旋转和平移的坐标变换。)
3、 To discover how several transformation matrices can be combined into one net transformation matrix through matrix-matrix multiplication.(知道为何几个变换矩阵可以通过矩阵之间的乘积来结合成一个矩阵。)
4、 To find out how we can convert coordinates from one coordinate system to another, and how this change of coordinate transformation can be represented by amatrix.(发现如何将坐标从一个坐标系变到另一个坐标系,以及这个坐标变换矩阵如何由矩阵表示。)
5、 To become familiar with the subset of functions provided by the XNA Math library used for constructing transformation matrices.(熟悉XNA Math库所提供的关于构造变换矩阵的那部分函数。)
这一章的内容和“龙书”第二版的第3章还是比较对应的,不过没有提到射线和平面的内容。相比龙书来说,这一章没有特别需要注意的内容,我就将重点以一个简单的列表形式列在下面了:
1、 第3.2.1节Homogeneous Coordinates(齐次坐标)这一小节提出了齐次坐标的概念。这一概念很重要,是后面我们进一步学习3D图形学的基础。
2、 第3.5节Transformation Matrix versus Change of Coordinate Matrix(变换矩阵与坐标变换矩阵)说明 “active” transformations和change of coordinate transformations是可以等同视之的。之所以这样可能有点违反我们的直觉,并且可能和我们所接收到的数学教育不一样;这里我给一下我的个人理解。以前我觉得坐标变换和对物体本身的变换是不一样的,因为坐标变换会改变整个空间中所有物体的坐标,而物体本身的变换只改变物体自身的坐标;但是在3D游戏编程中,物体是“离散”的,空间中并没有充斥着“致密的点”(打个比方:现实世界中,空气中充满了尘埃,所以在黑暗环境中打开手电筒可以看见一道光束;但是在3D游戏世界中,我们并不能够很轻易地看到光柱,只能通过一些技巧来达到光束的效果。在3D游戏世界中,灯光是通过与实在的物体——比如说一个游戏角色——相互作用所表现出来的,我们并不能看到“光”本身),整个3D世界是由有限个物体(每个物体由有限个顶点组成)组成的,我们一般要为每个物体指定一个世界矩阵(世界矩阵以后会讲到),而世界矩阵本质上是坐标变换,但是在3D游戏中实际上等同于物体的“active” transformations。
3、 第3.6节XNA MathTransformation Functions(XNA Math 变换函数)列出了与变换相关的XNA函数以供参考。书上没有给出具体的例子,不过后面的习题会让你有机会使用的。
===============================================================================
勘误:
===============================================================================
1、 在第3.1.4节的例3.3前的式子中,三个旋转矩阵都以4x4维的形式表示了。尽管是正确的,但是这个现在出现得不合时宜,读者此时可以将这三个矩阵的第4行和第4列去掉,只保留前3行和前3列。
2、 第3.2.4节的公式(eq. 3.7):
中,中间的列向量形式的矩阵应该是4x4维的,所以其实应该补充第4列——[0, 0, 0, 1]的转置。
3、 第3.2.4节的图3.8右边有一个向量的箭头画反了,应该是这样的(来自于书本附带的DVD中的高清彩图):
4、 习题部分第19题最后一句话的conjecturer 写错了,应该是conjecture。
===============================================================================
习题解答:
===============================================================================
与上一章一样,这一章的习题大部分是数学题(这种情况后面比较少,但是并没有绝迹)。
1-17题:
太简单了,从略。
18-19题:
第18题提出了一个质心(barycenter)的概念,使得点也能够像向量一样进行加法运算(当然系数是限制的,否则就不能满足“运算结果仍然是点”的要求了)。第19题是第18题的承接。
20题:
这道题让我们证明线性映射的一个比较好的性质:它保持线性组合。这道题很简单,使用定义,然后用数学归纳法证明就行了。
21-24题:
很简单,从略。
25题:
提出了判断一个(应该限制在2、3和4维的方)矩阵是旋转矩阵的充要条件,然后让我们用这个充要条件去证明一些简单的结论。这一题可能要用到第2章的习题14中给出的一个结论。
26题:
让我们继续证明关于旋转矩阵的一些性质。也不难。
27题:
这道题可能有点难度。其实窍门就是按照缩放-旋转-平移的顺序构造变换矩阵就行了。这种方法在我们以后的游戏编程例子中会经常见到的。
28题:
让我们找到一种对长方形进行“原地缩放”的方法。也很简单。
===============================================================================
PS:可能大家会发现这几章的习题部分讲得太简略了。不过请放心,后面的那些要求写代码的习题我都是不会放过的,哈哈!
好啦,这一期就到这里了,咱们下期再见!