树形DP集锦
FZU 2038 (树上任意2点距离,总和)
http://acm.fzu.edu.cn/problem.php?pid=2038
给一颗树, 求任意2点距离的总和。
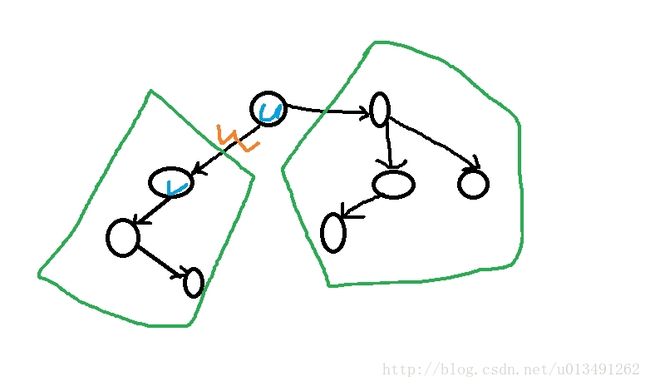
如图, 对于(u-> v , w)
f(v) = v的子树节点个数,(含自己)。
那么经过w , 总和为。 f(v) * (N - f(v)) * w 。
方向,绿色1 -> 绿色2 。 绿色2->绿色1 。 最后结果*2 。
const int Max_N = 100008 ;
struct Edge{
int v ;
int w ;
int next ;
}edge[Max_N<<1] ;
int List[Max_N] ;
int id ;
void add_edge(int u , int v , int w){
edge[id].v = v ;
edge[id].w = w ;
edge[id].next = List[u] ;
List[u] = id++ ;
}
int N ;
LL ans ;
int dp[Max_N] ;
int dfs(int u , int father){
int e , v , w , sonnode ;
dp[u] = 1 ;
for(e = List[u] ; e != -1 ; e = edge[e].next){
v = edge[e].v ;
w = edge[e].w ;
if(v == father)
continue ;
sonnode = dfs(v , u) ;
ans += (LL)w * (LL)sonnode * LL(N - sonnode);
dp[u] += sonnode ;
}
return dp[u] ;
}
int main(){
int T ,i , cas , u , v , w ;
scanf("%d" ,&T) ;
for(cas = 1 ; cas <= T ; cas++){
scanf("%d" ,&N) ;
id = 0 ;
memset(dp , 0 , (1+N)*sizeof(int)) ;
memset(List, -1 , (1+N)*sizeof(int)) ;
for(i = 1 ; i < N ; i++){
scanf("%d%d%d" ,&u ,&v ,&w) ;
add_edge(u , v , w) ;
add_edge(v , u , w) ;
}
ans = 0 ;
dfs(0 , -1) ;
printf("Case %d: " , cas) ;
cout<<(ans<<1)<<endl ;
}
return 0 ;
}
HDU 1561
http://acm.hdu.edu.cn/showproblem.php?pid=1561
一颗树,N个节点,每个节点权值w . 选取相连的M个节点,使得最大加权和。
const int Max_N = 208 ;
vector<int> List[Max_N] ;
int N , M ;
int dp[Max_N][Max_N] ;
void dfs(int u){
int i , v , j , k ;
for(i = 0 ; i < List[u].size() ; i++){
v = List[u][i] ;
dfs(v) ;
for(j = M ; j >= 2 ; j--){
for(k = 1 ; k < j ; k++)
dp[u][j] = max(dp[u][j] , dp[u][k] + dp[v][j-k]) ;
}
}
}
int main(){
int u , v , i ;
while(scanf("%d%d" ,&N , &M) , N+M){
memset(dp , 0 , sizeof(dp)) ;
for(i = 0 ; i <= N ; i++) List[i].clear() ;
for(v = 1 ; v <= N ; v++){
scanf("%d" ,&u) ;
List[u].push_back(v) ;
scanf("%d" ,&dp[v][1]) ;
}
M++ ;
dfs(0) ;
printf("%d\n" , dp[0][M]) ;
}
return 0 ;
}
URAL 1018
http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=17662
一颗树,N个节点,N-1条边,每条边权值w . 选取相连的M条边,使得最大加权和。
const int Max_N = 108 ;
struct Edge{
int v ;
int w ;
Edge(){}
Edge(int i , int j):v(i) , w(j){}
};
vector<Edge> List[Max_N] ;
int N , M ;
int dp[Max_N][Max_N] ;
int dfs(int u , int father){
int i , j , k , v , w , sonedge = 0 ;
for(i = 0 ; i < List[u].size() ; i++){
v = List[u][i].v ;
w = List[u][i].w ;
if(v == father)
continue ;
sonedge += dfs(v , u) + 1 ;
for(j = M ; j >= 1 ; j--){
for(k = 1 ; k <= j ; k++)
dp[u][j] = max(dp[u][j] , dp[u][j-k] + dp[v][k-1] + w) ;
}
}
return sonedge ;
}
int main(){
int i , u , v , w ;
while(scanf("%d%d" ,&N ,&M) != EOF){
memset(dp , 0 , sizeof(dp)) ;
for(i = 1 ; i <= N ; i++) List[i].clear() ;
for(i = 1 ; i < N ; i++){
scanf("%d%d%d" ,&u ,&v ,&w) ;
List[u].push_back(Edge(v ,w)) ;
List[v].push_back(Edge(u ,w)) ;
}
dfs(1 , -1) ;
printf("%d\n" ,dp[1][M]) ;
}
return 0 ;
}
N个节点,N-1条边, 求到其他所有点的距离之和最小的全部点与距离
typedef long long LL ;
const int Max_N = 50008 ;
vector<int>List[Max_N] ;
LL N , I , R ;
LL dp[Max_N] , sum[Max_N] , ans[Max_N] ;
int dfs(int u , int father){
int i , v ;
dp[u] = 1 ;
for(i = 0 ; i < List[u].size() ; i++){
v = List[u][i] ;
if(v == father)
continue ;
dp[u] += dfs(v , u) ;
sum[u] += dp[v] + sum[v];
}
return dp[u] ;
}
void dfs_2(int u , int father){
int i , v ;
for(i = 0 ; i < List[u].size() ; i++){
v = List[u][i] ;
if(v == father)
continue ;
ans[v] = ans[u] - (sum[v] + dp[v]) + (N - dp[v]) + sum[v] ;
dfs_2(v , u) ;
}
}
int main(){
int T , u , v , i ;
scanf("%d" ,&T) ;
while(T--){
cin>>N>>I>>R ;
for(i = 1 ; i <= N ; i++){
List[i].clear() ;
dp[i] = 0 ;
sum[i] = 0 ;
ans[i] = 0 ;
}
for(i = 1 ; i < N ; i++){
scanf("%d%d" ,&u ,&v) ;
List[u].push_back(v) ;
List[v].push_back(u) ;
}
dfs(1 , -1) ;
ans[1] = sum[1] ;
dfs_2(1 , -1) ;
vector<int> result ;
result.clear() ;
LL min_len = ans[1] ;
for(i = 1 ; i <= N ; i++){
if(min_len > ans[i])
min_len = ans[i] ;
}
for(i = 1 ; i <= N ; i++){
if(ans[i] == min_len)
result.push_back(i) ;
}
cout<<min_len*I*I*R<<endl ;
printf("%d" ,result[0]) ;
for(i = 1 ; i < result.size() ; i++)
printf(" %d" ,result[i]) ;
puts("") ;
puts("") ;
}
return 0 ;
}
HDU 4276 n个点,n-1条边,每条边有边劝,每个点有点权(表示走每条边的时间),问在时间T从点1走到点n,能够得到最大的点权和。
思想: 1 - > N 路径唯一, 那么这条路必须经过。 记这条路需要花的时间为T1, 则剩下T- T1 。
T-T1 ,时间内 从1 - >其他点 - > 1 。必须回到起点1 。 这就相当于 1 - >N 的情况。
转化成了经典的树形背包模型。
const int Max_N = 108 ;
const int inf = (1<<30) ;
struct Edge{
int v ;
int w ;
int next ;
};
Edge edge[Max_N<<1] ;
int grid[Max_N][Max_N] ;
int List[Max_N] ;
int id ;
int prefather[Max_N] , bao[Max_N] ;
void add_edge(int u , int v , int w){
edge[id].v = v ;
edge[id].w = w ;
edge[id].next = List[u] ;
List[u] = id++ ;
}
int N , T ;
int dp[Max_N][508] ;
void dfs_1(int u , int father){
int e , v , w ;
if(u == N)
return ;
for(e = List[u] ; e != -1 ; e = edge[e].next){
v = edge[e].v ;
if(v == father)
continue ;
prefather[v] = u ;
dfs_1(v , u) ;
}
}
void dfs(int u , int father){
int e , v , w ;
for(e = List[u] ; e != -1 ; e = edge[e].next){
v = edge[e].v ;
w = edge[e].w ;
if(v == father)
continue ;
dfs(v , u) ;
for(int i = T ; i >= w ; i--)
for(int j = 0 ; j <= i - w ; j++)
dp[u][i] = max(dp[u][i] , dp[u][i-w-j] + dp[v][j]) ;
}
for(int i = 0 ; i <= T ; i++)
dp[u][i] += bao[u] ;
}
int main(){
int i , j , u , v , w , mustlen ;
while(scanf("%d%d" ,&N ,&T) != EOF){
id = 0 ;
memset(List , -1 , sizeof(List)) ;
for(i = 1 ; i <= N ; i++)
for(j = 1 ; j <= N ; j++)
grid[i][j] = inf ;
for(i = 1 ; i < N ; i++){
scanf("%d%d%d" ,&u ,&v ,&w) ;
add_edge(u , v , w) ;
add_edge(v , u , w) ;
grid[u][v] = grid[v][u] = w ;
}
memset(dp , 0 , sizeof(dp)) ;
for(i = 1 ; i <= N ; i++)
scanf("%d" ,&bao[i]) ;
memset(prefather , -1 , sizeof(prefather)) ;
dfs_1(1 , -1) ;
u = N ;
mustlen = 0 ;
while(u != -1){
v = prefather[u] ;
mustlen += grid[u][v] ;
if(v != -1){
grid[u][v] = grid[v][u] = 0 ;
}
u = v ;
}
if(mustlen > T){
puts("Human beings die in pursuit of wealth, and birds die in pursuit of food!") ;
continue ;
}
id = 0 ;
memset(List , -1 , sizeof(List)) ;
for(i = 1 ; i <= N ; i++){
for(j = 1 ; j <= N ; j++){
if(grid[i][j] != inf)
add_edge(i , j , 2*grid[i][j]) ;
}
}
T -= mustlen ;
dfs(1 , -1) ;
printf("%d\n" ,dp[1][T]) ;
}
return 0 ;
}
求任意2个叶子节点的最短距离。
HDU 3848 http://acm.hdu.edu.cn/showproblem.php?pid=3848
const int Max_N = 10008 ;
struct Edge{
int v ;
int w ;
int next ;
}edge[Max_N*2];
int N ;
int id ;
int List[Max_N] , dp[Max_N] ;
int ans ;
void add_edge(int u , int v , int w){
edge[id].v = v ;
edge[id].w = w ;
edge[id].next = List[u] ;
List[u] = id++ ;
}
int dfs(int u , int father){
int e , v , w , son = 0 ;
dp[u] = 0 ;
for(e = List[u] ; e != -1 ; e = edge[e].next){
son++ ;
v = edge[e].v ;
w = edge[e].w ;
if(v == father) continue ;
dfs(v , u) ;
if(dp[u] == 0)
dp[u] = dp[v] + w ;
else{
ans = min(ans , dp[u] + dp[v] + w) ;
dp[u] = min(dp[u] , dp[v] + w) ;
}
}
if(u == 1 && son == 1)
ans = min(ans , dp[1]) ;
return dp[u] ;
}
int main(){
int u , v , w , i ;
while(cin>>N && N){
memset(List , -1 , sizeof(List)) ;
id = 0 ;
for(i = 1 ; i < N ; i++){
scanf("%d%d%d" ,&u , &v , &w) ;
add_edge(u , v , w) ;
add_edge(v , u , w) ;
}
ans = 1<<30 ;
dfs(1 , -1) ;
cout<<ans<<endl ;
}
return 0 ;
}
N个点,N-1条边,给你K个机器人从s点出发,每条路有一定的权值,求历遍整棵树最小的权值和。
http://acm.hdu.edu.cn/showproblem.php?pid=4003
const int Max_N = 10008 ;
struct Edge{
int v ;
int w ;
Edge(){}
Edge(int _v , int _w):v(_v) ,w(_w){}
};
vector<Edge> List[Max_N] ;
int N , K , S ;
int dp[Max_N][11] ;
void dfs(int u , int father){
int e , i , v , w , j;
for(e = 0 ; e < List[u].size() ; e++){
v = List[u][e].v ;
w = List[u][e].w ;
if(v == father) continue ;
dfs(v , u) ;
for(i = K ; i >= 1 ; i--){
dp[u][i] += dp[v][0] + 2*w ;
for(j = 1 ; j <= i ; j++)
dp[u][i] = min(dp[u][i] , dp[v][j] + j*w + dp[u][i-j]) ;
}
dp[u][0] += dp[v][0] + 2*w ;
}
}
int main(){
int i , u , v , w ;
while(scanf("%d%d%d" ,&N , &S , &K) != EOF){
for(i = 1 ; i <= N ; i++) List[i].clear() ;
for(i = 1 ; i < N ; i++){
scanf("%d%d%d" ,&u ,&v ,&w) ;
List[u].push_back(Edge(v , w)) ;
List[v].push_back(Edge(u , w)) ;
}
memset(dp , 0 , sizeof(dp)) ;
dfs(S , -1) ;
printf("%d\n" , dp[S][K]) ;
}
return 0 ;
}