K近邻快速算法 -- KD树、BBF改进算法

K近邻算法即是查找与当前点（向量）距离最近的K个点（向量），距离计算一般用欧氏距离。

最简单的方法就是穷举法：计算每个向量与当前向量的欧氏距离，选取最小的K个为所求。但这种方法计算量太大，无法应对大样本数的情况（比如SIFT特征点匹配，每张图片一般有几千个待匹配的特征点，对每个点都需要查找另一张图片中与之最相似的特征点从而建立对应关系，穷举法显然不行）。

SIFT采用的方法是：先将所有特征向量进行预处理，组成KD树的结构（二叉树），仅计算KD树中可能路径下（使用了BBF改进算法计算路径）特征向量的欧式距离，从而减小计算量。

本文将首先介绍KD树的构造，然后介绍KD树下的最近邻查找，最后介绍KD树下改进的查找方法BBF。

KD树的构造

KD树（k-dimension tree）是对数据点在K维空间中划分的一种数据结构

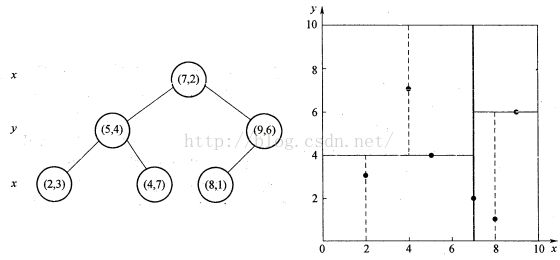
假设对于6个二维数据点（此时K=2）：{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}

（1）计算所有数据每一维的方差

在这里即计算(2, 5, 9, 6, 4, 7, 8)和(3, 4, 6, 7, 1, 2)的方差，分别为39和28.63

方差大的那一维（在这里为x轴）意味着当前数据在这一维分布最为分散，因此首先将数据按这一维进行划分

（2）选取方差最大的那一维中所有数据的中位数作为分割超面（根节点）

在这里选第一维（X轴）的数据，中位数为7，因此将x=7作为第一个分割超平面（点(7,2)作为根节点）

取中位数的好处是，能尽量保证左右子树的节点数平衡

（3）确定左子树右子树

经过（2）后，按x=7可将数据分成左子树：{(2,3), (5,4), (4,7)}和右子树：{(9,6), (8,1)}

然后分别对左右子树从（1）开始做递归，直到叶子节点

图1-1. KD树（左）和空间划分图（右）（截自《图像局部不变性特征与描述》）

注：考虑到计算方差增加的计算量，也有一种做法是：轮流选取维度进行划分（首先按第1维，KD树的第2层按第2维...）。显然这种方法分割得到的结果可区分度没有方差法好。

基于KD树的最近邻查找

还是以上一节的数据为例，假设待查找的数据是(2, 4.5)

（1）生成搜索路径

从根节点开始，按该层的分割面逐层向下搜索，直到叶节点

在这里首先比较(7,2)，由于是按X轴划分，而2<7，因此搜索左节点(5,4)， 该节点是按Y轴划分，而4.5>4，因此搜索右节点(4,7)。由于(4,7)已是 叶节点，搜索结束，得到搜索路径 (7,2)->(5,4)->(4,7)

记(4,7)为当前最近邻，计算两点的欧式距离3.2，为最近距离

（2）回溯

显然按（1）并不一定能得到全局最近邻，因此需要按路径回溯查找

首先判断当前点另一兄弟节点是否需要访问（KD树就是通过这种方式节省匹配时间的）：如果已访问过或者当前点与该层分割面的距离大于当前最近距离，则放弃访问其兄弟分支，回溯至其父节点。

在这里(2,4.5) 与y=4的距离为0.5，小于3.2，因此需要搜索其左兄弟节点(2,3)，计算(2,4.5)与(2,3)的距离1.5<3.2，因此更新最近邻为(2,3)，最近距离为1.5；然后回溯至(5,4)，由于(2,4.5)与x=7的距离为5，大于1.5，因此其右兄弟分支(9,6)不再搜索，最后回溯至(7,2)，结束。该过程一共比较了4次。

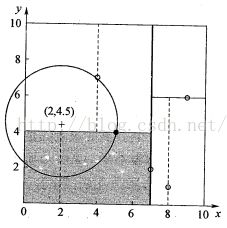
图1-2. 以当前点为圆心，最近距离为半径画超圆，如果与分割超平面相交则搜索兄弟分支

KD树BBF快速搜索算法

KD树最近邻查找算法在回溯过程中通过计算超圆与超平面的距离决定是否比较兄弟分支，这在维数较低的时候能有效减小计算量；但当维数较高时（比如SIFT有128维）由于需要比较的分支太多，到最后基本上每个数据点都做了比较（与穷举法一样了），加上构建KD树的时间，此时算法性能甚至不如穷举法。

对K维的N个数据（节点），KD树最近邻查找算法的时间复杂度为，一般只有在数据规模和维度满足时才能保证该算法的高效。

Lowe等人（没错，提出SIFT的那伙人）提出的BBF（Best Bin First）方法，建立了一个优先序列，每次在优先序列里比较，通过限定最大比较次数/超时（我认为这是算法提速的核心），达到提高搜索效率的目的。该算法得到的解不一定是最优解，属于牺牲精度换效率的思路。

（1）首先从根节点开始，按上节方式生成搜索路径，同时计算路径下每个节点与(2,4.5)的距离，将该节点的兄弟节点压入优先序列

搜索路径：(7,2)->(5,4)->(4,7)，优先序列：{(2,3), (9,6)}，最近点(5,4)

（2）提取优先序列中优先级最高的点(2,3)，以该点为“根节点”，重复（1）

可以看到，BBF实现了按可能性排序的查询方式，然后通过限定次数来截断搜索（否则又与原始算法一样了），达到了快速检索的目的。

代码

https://github.com/sdeming/kdtree实现了基本的KD树及搜索，需要注意的是，其KD树的分割是按照维度轮流的方式实现的。

Rob Hess实现的SIFT算法中实现了BBF版的KD树算法

参考

[1] 《图像局部不变性特征与描述》

[2] Kd Tree算法原理和开源实现代码