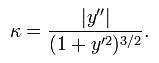Spline导数及曲率计算
1 概述
曲率的公式为:
因此求曲率的重点在于获得拟合曲线的一阶导数和二阶导数。
2 Matlab中的实现
2.1 实例1
根据参考资料[5]的提示,可以使用csape()对离散点进行Spline插值,然后使用fnder()对得到Spline曲线求导,最后使用fnval()对导数求值即可。
%% 原数据
x = 0 : 0.1 : 2 * pi;
y = sin(x);
plot(x, y, 'o')
%% spline拟合
pp = csape(x, y);
%% 拟合图
hold on
plot( x, fnval(pp, x), 'g' );
%% 求导
pp1 = fnval(fnder(pp, 1), x); %求一阶导
pp2 = fnval(fnder(pp, 2), x); %求二阶导
%% 曲率,K = |y''| / ((1 + y'^2)^(3/2))
curvature = abs(pp2) ./ sqrt( (1 + pp1 .^ 2) .^ 3 );
%% 曲率图
hold on
plot( x, curvature, 'r' );
%% 图例
legend('原始散点', 'Spline拟合结果', '曲率图');
%% 显示网格
grid on
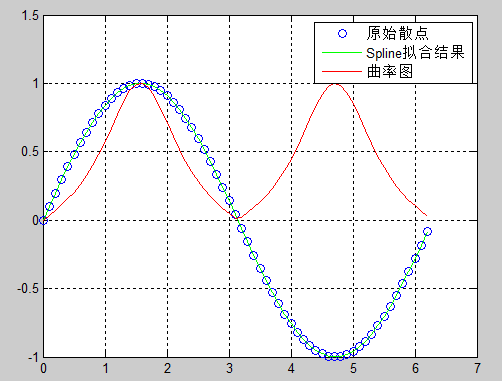
上述代码的运行结果如下图所示:
2.2 实例2
参考资料[11]给出了另外一个实例:
%% 原始数据点
xx=[-1 0 3 5 8 9 ];
yy=[1 7 -4 0 7 3 ]; %给定6个点
%% spline拟合
sp = spline(xx,yy); % spline(x,y) 曲线插值
x = xx(1):0.01:xx(length(xx)); %通常取x(1)至x(n)
y = ppval(x,sp); % ppval( , ) 分段多项式的值 y的值变为数组y()
subplot(311)
for i=1:length(xx)
plot(xx(i), yy(i),'b*')
hold on
end
plot(x,y,'r');
grid on
title('B样条插值曲线')
%% 斜率计算
for i=1:(length(x)-1)
dx(i)=x(i+1)-x(i);
dy(i)=y(i+1)-y(i); % 离散一次导(相当于连续一次导数)
dddy(i)= dy(i)/dx(i);
end
%% 曲率计算
for i = 1 : (length(x)-2)
ddx(i) = dx(i+1) - dx(i);
ddy(i) = dy(i+1) - dy(i); % 离散二次差分(相当于连续二次导)
K(i)=(dx(i)*ddy(i)-dy(i)*ddx(i))/((dx(i)*dx(i)+dy(i)*dy(i))^1.5); % 曲率
end
subplot(312)
ud=linspace(xx(1),xx(length(xx)),(length(x)-1));
plot(ud,dddy)
grid on
title('曲线斜率变化图')
subplot(313)
uu=linspace(xx(1),xx(length(xx)),(length(x)-2));
plot(uu,K)
grid on
title('曲线曲率变化图')
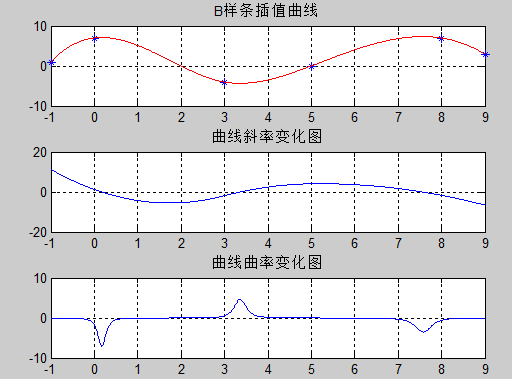
上述代码执行效果如下图:
参考资料
[1]三次B样条曲率与导数算法Matlab代码
[2]样条曲线
[3]B样条曲线曲率简易求解算法
[4]如何用matlab提取曲线各点曲率
[5]如何得到matlab三次样条曲线插值(csape)之后得到的拟合曲线的曲率图
[6]用matlab求出最小曲率半径曲线方程实例
[7]对离散样点做三次样条曲率计算和求导的matlab程序
[8]知道一些坐标,怎么用matlab画出曲线并计算出曲线的曲率
[9]计算曲率
[10]用MATLAB求曲线在某一点的曲率
[11]对给定的离散点,先拟合成B样条曲线,再求B样条曲线曲率
[12]Curvature of a spline
[13]Curvature of Approximating Curve Subdivision Schemes