Dijsktra算法原理介绍及java源码实践
Dijsktra是典型的最短路径算法,也是最古老的算法。
目的:用于计算一个节点到其他节点的最短路径。
主要特点:以起始点为中心,层层向外扩展(广度搜索思想),直到扩展到所求节点为止。
基本步骤:
1、指定起始点S,以及各节点之间路径值,不相同的节点路径值用∞表示。个节点之间的距离一般用邻接矩阵表示。
2、引进两个集合,Open表示还未计算出最短路径的节点集合,保存未计算节点路径值;Closed表示已计算出最短路径的节点集合,保存已计算节点的最短路径值。
3、从Closed选出最短节点K,放入Open,并从Closed移除节点K。
4、更新Closed中各节点到起始点S的距离。
5、重复步骤3、4,直到遍历到所求节点加入Open,即得S到所求节点的最短距离。
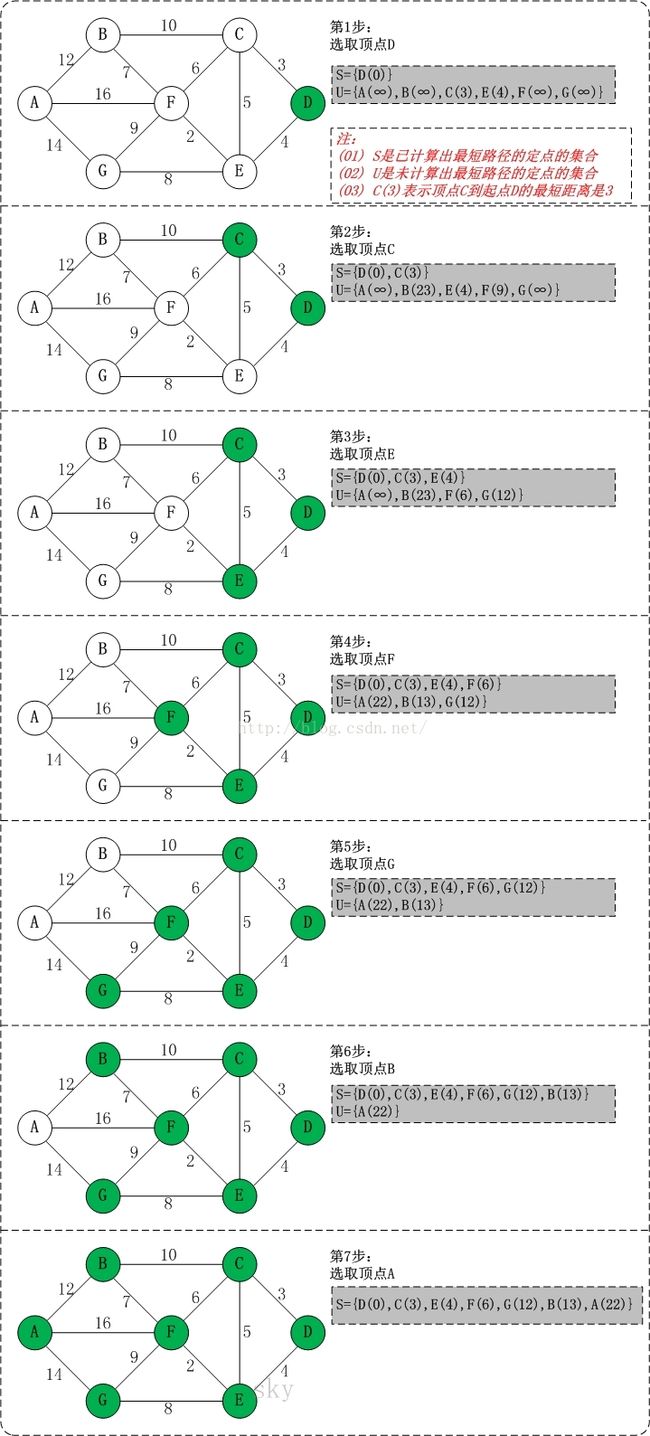
算法执行过程见下图:
算法java源码如下:
public class Dijsktra {
private static int M = 10000; // 没有连接线路
public static void main(String[] args) {
int[][] weight1 = { { 0, 3, 2000, 7, M }, // 邻接矩阵:五个顶点之间的距离
{ 3, 0, 4, 2, M },
{ M, 4, 0, 5, 4 },
{ 7, 2, 5, 0, 6 },
{ M, M, 4, 6, 0 } };
int[][] weight2 = { { 0, 10, M, 30, 100 },
{ M, 0, 50, M, M },
{ M, M, 0, M, 10 },
{ M, M, 20, 0, 60 },
{ M, M, M, M, 0 } };
int start = 0;
int[] shortPath1 = dijkstra(weight2, start);
for (int i = 0; i < shortPath1.length; i++)
System.out.println("从" + start + "出发到" + i + "的最短距离为:" + shortPath1[i]);
// int[] shortPath2 = dijkstra(weight2, start);
// for (int i = 0; i < shortPath2.length; i++)
// System.out.println("从" + start + "出发到" + i + "的最短距离为:" + shortPath2[i]);
}
public static int[] dijkstra(int[][] weight, int start) {
int n = weight.length; // 顶点个数
int[] shortPath = new int[n]; // 保存start到其他各点的最短路径
String[] path = new String[n]; // 保存start到其他各点最短路径的字符串表示
for (int i = 0; i < n; i++)
path[i] = new String(start + "-->" + i);
int[] visited = new int[n]; // 标记当前该顶点的最短路径是否已经求出,1表示已求出
shortPath[start] = 0; // 初始化,第一个顶点已经求出
visited[start] = 1;
for (int count = 1; count < n; count++) { // 要加入n-1个顶点
int k = -1; // 选出一个距离初始顶点start最近的未标记顶点
int dmin = Integer.MAX_VALUE;
for (int i = 0; i < n; i++) {
if (visited[i] == 0 && weight[start][i] < dmin) {
dmin = weight[start][i];
k = i;
}
}
// 将新选出的顶点标记为已求出最短路径,且到start的最短路径就是dmin
shortPath[k] = dmin;
visited[k] = 1;
// 以k为中间点,修正从start到未访问各点的距离
for (int i = 0; i < n; i++) {
if (visited[i] == 0 && weight[start][k] + weight[k][i] < weight[start][i]) {
weight[start][i] = weight[start][k] + weight[k][i];
path[i] = path[k] + "-->" + i;
}
}
}
for (int i = 0; i < n; i++) {
System.out.println("从" + start + "出发到" + i + "的最短路径为:" + path[i]);
}
System.out.println("=====================================");
return shortPath;
}
}
从0出发到0的最短路径为:0-->0
从0出发到1的最短路径为:0-->1
从0出发到2的最短路径为:0-->3-->2
从0出发到3的最短路径为:0-->3
从0出发到4的最短路径为:0-->3-->2-->4
=====================================
从0出发到0的最短距离为:0
从0出发到1的最短距离为:10
从0出发到2的最短距离为:50
从0出发到3的最短距离为:30
从0出发到4的最短距离为:60