动态树（Link-Cut Tree）学习小结

动态树（LCT）支持合并分离等操作，是一棵可以动的树~

类似于树链剖分（建议先学完树链剖分，再学LCT）。

只不过树链剖分的轻重边是根据子树大小而决定的，这棵树只能是静态的。

而LCT中的“轻重边”是根据最后一次操作决定的，最后一次处理了x这个点，那么从x到根的路径就是重链（每个父亲只与一个儿子的连边为重边）。

用splay来维护每一条重链，以点的深度为关键字，即splay中的每个点左儿子深度都比他小，右儿子的深度都比他大（若只有一个点，那么这个点单独是一棵splay）。

先来定义一些量：

1.Preferred child：

如果一个点是他父亲结点的所有儿子中最后被访问的，那么他是他父亲的Preferred child。

每个点最多有一个Preferred child。

如果x结点是最后被访问的点，那么他没有Preferred child。

2.Preferred edge:

每个点到自己的Preferred child的边叫Preferred edge（相当于树链剖分中的重边）

3.Preferred path:

由Preferred edge组成的链叫Preferred path（相当于树链剖分的重链）

代码中的：

1.root[x]

表示x是否是他所在splay的根

2.l,r

左,右儿子

3.fa

父亲

4.rev

区间是否被反转

接下来说一下LCT的基本操作：

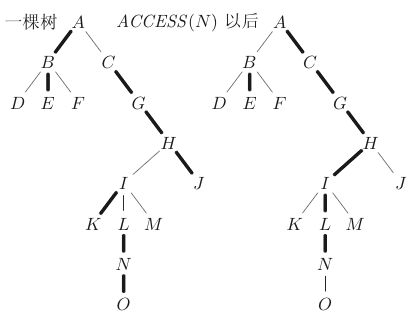
（一）Access(x)

LCT的最基础操作，使x到根结点的路径成为重链。

如上图，粗边为重边。

具体应该怎么操作呢？

首先把x旋到他所在的splay的根部。

因为当前的x点是最后一个被访问的点，所以他没有Preferred child，因此要把右儿子与他断开，右儿子成为新的一条链，那么x该往哪儿连？

x的父亲是y，把y旋到他所在splay的根结点，把此时y的右儿子与他断开，把x连过来即可，相当于合并y和x所在的splay。
然后，再找y的父亲，合并y与y的父亲所在的splay。。。。。一直到根结束。

最终，x到根结点的路径成为新的Preferred edge，而曾经的Preferred child都被抛弃。。

void Access(int x)
{
	int y=0;
	while (x)
	{
		Splay(x);
		root[a[x].r]=1;
		a[x].r=y;
		root[a[x].r]=0;
		y=x;
		x=a[x].fa;
	}
}

（二）Makeroot(x)

使x成为整棵树的根。


首先Access（x），这样x与根结点处在同一棵splay中。

然后splay（x），x成为这棵splay的根。显然，x只有左儿子。

因为要让x成为整棵树的根，所以x的深度要最小，那么，我们只要一个区间反转的标记rev就可以完成。

void Makeroot(int x)
{
	Access(x);
	Splay(x);
	a[x].rev^=1;
}

（三）Link（x,y）

连接x与y所在的两棵树。

首先Makeroot(x)，x就成为了他所在树的根。

然后直接把x的父亲赋值为y即可。

void Link(int u,int v)
{
	Makeroot(u);
	a[u].fa=v;
}

（四）Cut（x,y）

断开x与y所相连的边。

首先Makeroot(x)，然后Access(y)，此时x与y在同一棵splay中，再Splay(y)，此时x是y的左儿子。

然后通过改变父亲等操作就断开了。

void Cut(int u,int v)
{
	Makeroot(u);
        Access(v);
	Splay(v);
	root[a[v].l]=1;
	a[a[v].l].fa=0;
	a[v].l=0;
}

感悟：

1.LCT相当于多棵splay被虚线连在一起；

对于一条实边，既有父亲指针也有儿子指针；对于一条虚边只有父亲指针，也就是只能自底向上访问。

而最开始的时候是N个单独的点与他的父亲用虚线相连，每个点是一棵splay。

2.无论树怎样旋转，怎样变换，读入时所连接的边（没有被Cut的），一直都连着的

3.在每棵splay中每一个结点左子树中的节点都是他在原树中的祖先，右子树中的结点都是他在原树中的孩子；

所以虚线表示当前splay中深度最小的点与上面一棵splay某个点相连