hihocder 1181 : 欧拉路·二
因为相连的两个数字总是相同的,不妨我们只写一次,那么这个例子可以写成:3-2-4-3-5-1。6个数字刚好有5个间隙,每个间隙两边的数字由恰好对应了一块骨牌。
如果我们将每一个数字看作一个点,每一块骨牌看作一条边。你觉得是怎么样的呢?
小Ho:以这个例子来说的话,就是:
要把所有的骨牌连起来,也就是把所有的边都走一次。咦,这不是欧拉路问题么!
小Hi:没错,这问题其实就是一个欧拉路的问题,不过和上一次不一样的在于,这一次我们要找出一条欧拉路径。
小Ho:那我们应该如何来找一条路径呢?
小Hi:我们还是借用一下上次的例子吧
使用我们上一次证明欧拉路判定的方法,我们在这个例子中找到了2条路径:
L1: 4-5-2-3-6-5 L2: 2-4-1-2
假设我们栈S,记录我们每一次查找路径时的结点顺序。当我们找到L1时,栈S内的情况为:
S: 4 5 2 3 6 5 [Top]
此时我们一步一步出栈并将这些边删除。当我们到节点2时,我们发现节点2刚好是L1与L2的公共节点。并且L2满足走过其他边之后回到了节点2。如果我们在这个地方将L2先走一遍,再继续走L1不就刚好走过了所有边么。
而且在上一次的证明中我们知道,除了L1之外,其他的路径L2、L3...一定都满足起点与终点为同一个点。所以从任意一个公共节点出发一定有一条路径回到这个节点。
由此我们得到了一个算法:
-
在原图中找一个L1路径
-
从L1的终点往回回溯,依次将每个点出栈。并检查当前点是否还有其他没有经过的边。若存在则以当前点为起点,查找L2,并对L2的节点同样用栈记录重复该算法。
-
当L1中的点全部出栈后,算法结束。
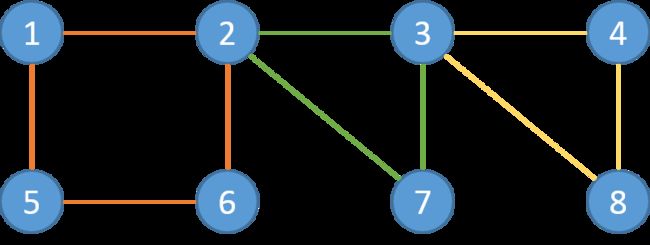
在这里我们再来一个有3层的例子:
在这个例子中:
L1: 1-2-6-5-1 L2: 2-3-7-2 L3: 3-4-8-3
第一步时我们将L1压入栈S,同时我们用一个数组Path来记录我们出栈的顺序:
S: [1 2 6 5 1] Path:
然后出栈到节点2时我们发现了2有其他路径,于是我们把2的另一条路径加入:
S: 1 [2 3 7 2] Path: 1 5 6
此时L2已经走完,然后再开始弹出元素,直到我们发现3有其他路径,同样压入栈:
S: 1 2 [3 4 8 3] Path: 1 5 6 2 7
之后依次弹出剩下的元素:
S: Path: 1 5 6 2 7 3 8 4 3 2 1
此时的Path就正好是我们需要的欧拉路径。
小Ho:原来这样就能求出欧拉路,真是挺巧妙的。
小Hi:而且这个算法在实现时也有很巧妙的方法。因为DFS本身就是一个入栈出栈的过程,所以我们直接利用DFS的性质来实现栈,其伪代码如下:
DFS(u): While (u存在未被删除的边e(u,v)) 删除边e(u,v) DFS(v) End PathSize ← PathSize + 1Path[ PathSize ] ← u
要注意,在DFS的时候,如果欧拉图当中存在奇数度的顶点,那么一定要从该顶点出发,如果没有,则任一点都行。。。。
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int n,m,edge[1001][1001],degree[1001]; int path[1001],len; void dfs(int u) { for(int i = 1; i <= n; i++) { if(edge[u][i] > 0) { edge[u][i]--, edge[i][u]--; dfs(i); } } path[len++] = u; } int main() { while(scanf("%d%d",&n,&m)!=EOF) { int u,v; memset(edge,0,sizeof(edge)); memset(degree,0,sizeof(degree)); for(int i = 1; i <= m; i++) { scanf("%d%d",&u,&v); edge[u][v]++, edge[v][u]++; degree[u]++, degree[v]++; } int k = 1; for(int i = 1; i <= n; i++) { if(degree[i] % 2 == 1) { k = i; break; } } len = 0; dfs(k); for(int i = len-1; i >= 0; i--) printf("%d ",path[i]); printf("\n"); } return 0; }