查找排序算法汇总

排序经常作为其他算法的辅助算法出现在各种场合，下面对排序来做一个汇总

（1）冒泡排序

思想：相邻的两个数比较，较小（大）的那个数向上移动（冒泡），而后最小（大）的数漂到最顶端

代码实现：

void BubbleSort(int *a,int size)
{
    int i,j;
    int t;
    bool bubble;
    for(i=0;i<size-1;i++)
    {
        bubble = false;  //若原序列为有序的，则会一次循环后就直接跳出循环，减少空比较次数
        for(j=0;j<size-1-i;j++)
        {
            if(a[j]>a[j+1])
            {
                t = a[j];
                a[j] = a[i];
                a[i] = t;
                bubble = true; 
            }
        }
        if(!bubble)
            break;
    }
}

冒泡排序的算法时间复杂度为O(N^2)

（2）直接选择排序

思想：通过n-i次比较，在i到n-1中选择最小的一个数，与i交换，这种算法虽然比较次数较多，但交换次数大为减少

代码实现：

void SelectSort(int *a,int size)
{
    int i,j;
    int t;
    int minnum;
    for(i=0;i<size-1;i++)
    {
        minnum = i;
        for(j=i;j<size-1;j++)
        {
            if(a[minnum]>a[j])
                minnum = j;
        }
        if(i!=minnum)
        {
            t = a[minnum];
            a[minnum] = a[i];
            a[i] = t;
         }
    }
}

算法时间复杂度为O(N^2)，略优于冒泡排序

 （3）直接插入排序

思想：在一个有序区中将待排序的数插入到适当位置，直至全部插入完毕

代码实现：

void InsertSort(int *a,int size)
{
    int i,j;
    int temp;
    for(i=1;i<size;i++)
    {
        if(a[i]<a[i-1])
        {
            temp = a[i];
            for(j=i-1;j>0&&a[j]>temp;j--)
            {
                a[j+1] = a[j];
            }
            a[j+1] = temp;
        }
    }
}

算法的时间复杂度为O（n^2）

 (4)锦标赛排序

思想： 锦标赛排序又叫树型排序，属于选择排序的一种。直接选择排序之所以不够高效就是因为没有把前一趟比较的结果保留下来，每次都有很多重复的比较。锦标赛排序就是要克服这一缺点。它的基本思想与体育淘汰赛类似，首先取得n个元素的关键字，进行两两比较，得到 n/2 个比较的优胜者，将其作为第一次比较的结果保留下来，然后对这些元素再进行关键值的两两比较，…，如此重复，直到选出一个关键字最小的对象为止。

代码实现及演示可参照：锦标赛排序详解

  （5）堆排序

思想：堆的定义类似于完全二叉树，小顶堆是父节点比任意子节点的关键字都小，并且其左右子堆满足同样的条件，大顶堆则相反。故堆排序利用了这种特性，对于大顶堆来说，其根节点是最大值，而后将其输出，其余各节点调整，成为一个新的大顶堆，依次将跟节点输出，则完成排序。

堆的存储使用数组来完成，对于父节点i，其两个子节点的的位置为2i+1,2i+2;对于一个子节点i，其父节点为(i-1)/2；

每次输出根节点后，将根节点的值与最后一个节点的值对换，则输出完毕后该数组变成有序数组。

代码实现：堆排序实现代码

算法时间复杂度：O（NlogN）

  (6)归并排序

思想：将A[0....N-1]分成两个子数组A1[0.....N/2], A2[N/2+1.......N-1]，分别对这两个数组进行单独排序，而后将这两个有序数组归并成一个有序数组

代码实现：

void mergeArray(int *a,int low,int mid,int high)
{
    int i = low;
    int j = mid+1;
    int size = 0;
    for(;(i<mid)&&(j<high);size++)
    {
        if(a[i]<a[j])
            temp[size] = a[i++];
        else
            temp[size] = a[j++];
    }
    while(i<mid)
        temp[size++] = a[i++];
    while(j<high)
        temp[size++] = a[j++];
    for(i=0;i<size;i++)
        a[low+i] = temp[i];
    
}
void mergeSort(int *a,int low,int high)
{
    if(low>high)return;
    int mid = (low+high)/2;
    mergeSort(a,low,mid);
    mergeSort(a,mid+1,high);
    mergeArray(a,low,mid,high);
}

  时间复杂度为：O（NlogN）；

  归并排序的两点改进：1）在数组比较短的时候可以不用递归，而是用插入排序或者选择排序；

  2）归并排序的过程中可以用记录数组下标的方式代替申请新的空间；从而避免A数组与辅助数组之间的频繁移动；

  （7）快速排序

思想：快速排序是一种基于划分的排序方法，在数组中取一个基准数，分区过程，将比该基准数小的数放到该数的前面，将比该基准数大的放到后面，而后对前后两个区再使用快速排序，直到排序完成。

代码实现：快速排序代码实现

算法的时间复杂度：O（NlogN）；

  （8）外排序

思想：外排序是指处理超过内存限度的数据的排序算法，通常是将中间结果放在外存上，外排序常采用“排序-归并”策略

    排序阶段，读入能放到外存上的数据量，将其排序输出到临时文件，依次进行，直到将待排序数组分成多个有序文件

    归并阶段，将这些临时文件合成一个大的有序文件

例：

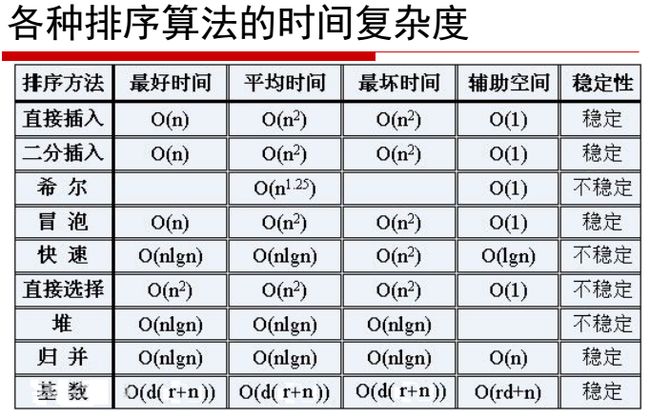
排序算法的分析：

这里的稳定是指 若未排序两个相等的关键字的前后位置在排序后与排序前前后位置相等，则称其为稳定的，若在比较的时候是相邻的数比较则最后结果是稳定的。

事实上，如果在排序的时候关键字和关键字所在在位置index同时参与排序，则不稳定算法可以转化成稳定算法