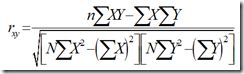图片识别前奏—计算两幅图片的皮尔逊相关系数

图片识别方法之一：颜色分步法

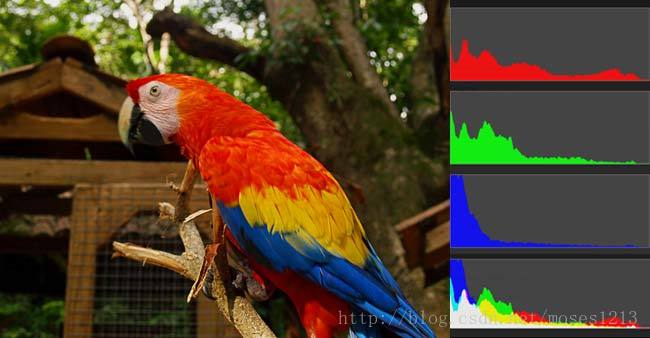
每张图片都可以生成颜色分布的直方图（color histogram）。如果两张图片的直方图很接近，就可以认为它们很相似。

任何一种颜色都是由红绿蓝三原色（RGB）构成的，所以上图共有4张直方图（三原色直方图 + 最后合成的直方图）。

如果每种原色都可以取256个值，那么整个颜色空间共有1600万种颜色（256的三次方）。针对这1600万种颜色比较直方图，计算量实在太大了，因此需要采用简化方法。可以将0～255分成四个区：0～63为第0区，64～127为第1区，128～191为第2区，192～255为第3区。这意味着红绿蓝分别有4个区，总共可以构成64种组合（4的3次方）。

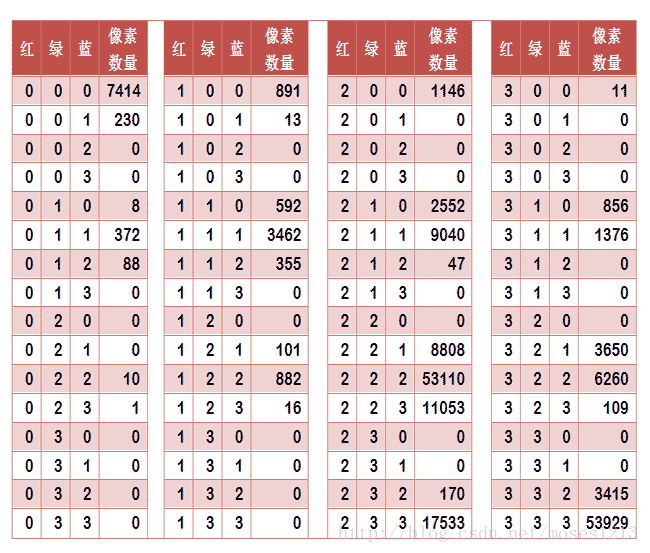
任何一种颜色必然属于这64种组合中的一种，这样就可以统计每一种组合包含的像素数量。

上图是某张图片的颜色分布表，将表中最后一栏提取出来，组成一个64维向量(7414, 230, 0, 0, 8, ..., 109, 0, 0, 3415, 53929)。这个向量就是这张图片的特征值或者叫"指纹"。

于是，寻找相似图片就变成了找出与其最相似的向量。这可以用皮尔逊相关系数或者余弦相似度算出。

皮尔逊相关系数回顾：

皮尔逊相关也称为积差相关（或积矩相关）是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。

假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：

公式一：

#include <cv.h>
#include <highgui.h>
#include <stdio.h>
#include <iostream>
#include <math.h>
using namespace std;
void histogram(IplImage* src, int color_histogram[], int N)
{
	int index;
	int width=src->width;
	int height=src->height;
	for (int w=0;w<width;w++)
	{
		for (int h=0;h<height;h++)
		{
			int Blue = ((uchar *)(src->imageData + h*src->widthStep))[w*src->nChannels +0];
			int Green = ((uchar *)(src->imageData + h*src->widthStep))[w*src->nChannels +1];
			int Red = ((uchar *)(src->imageData + h*src->widthStep))[w*src->nChannels +2];
			index = (Blue/64)*16+(Green/64)*4+(Red/64)*1;
			++color_histogram[index];
		}
	}
}
double math_coefficient(int a[], int b[], int N)
{
	double Sum_xy = 0;
	double Sum_x =0;
	double Sum_y = 0;
	double Sum_x2 = 0;
	double Sum_y2 = 0;
	for(int i=0; i<N; i++)
	{
		
		Sum_xy += a[i]*b[i];
		Sum_x += a[i];
		Sum_y += b[i];
		Sum_x2 += a[i]*a[i];
		Sum_y2 += b[i]*b[i];
	}

	return (Sum_xy*N-Sum_x*Sum_y)/sqrt((N*Sum_x2-pow(Sum_x,2))*(N*Sum_y2-pow(Sum_y,2)));
}
double image_coefficient(IplImage* src1, IplImage* src2)
{
	int H1[64] = {0};
	int H2[64] = {0};
	histogram(src1, H1,64);
	histogram(src2, H2,64);
	
	return math_coefficient(H1,H2,64);
}

int main()
{
	IplImage* src1 = cvLoadImage("D:\\opencv.JPG",1);
	IplImage* src2 = cvLoadImage("D:\\opencv_meitu_1.jpg",1);
	cout<<image_coefficient(src1,src2)<<endl;

	getchar();

	return 0;
}