算法学习之“Big Oh Notation”
一、Asymptotic analysis
Suppose we are considering two algorithms, A and B, for solving a given problem. Furthermore, let us say that we have done a careful analysis of the running times of each of the algorithms and determined them to be 
and 
, respectively, where n is a measure of the problem size. Then it should be a fairly simple matter to compare the two functions and to determine which algorithm is the best!
这段话的意识，比较两种算法的时间成本来判定哪种算法更好。但实际应用中，T(n)是随着问题的规模n变化的，在事先不知道n的情况下，没法比较两种算法的优劣。由此，引入“Asymptotic behavior”，比较两种算法的T(n)在n比较大时的“增长级数”，例如：对数增长、线性增长、指数级增长。
二、Big Oh notation
In 1892, P. Bachmann invented a notation for characterizing the asymptotic behavior of functions. His invention has come to be known as big oh notation:
Definition (Big Oh) Consider a function f( n) which is non-negative for all integers保罗.巴赫曼的“大O标记法”是最常用的一种算法 “Asymptotic behavior”的分析法（Asymptotic analysis）。它表示的是一种算法“Asymptotic behavior”的上界（upper bound）。. We say that `` f( n) is big oh g( n),'' which we write f( n)= O( g( n)), if there exists an integer
and a constant c>0 such that for all integers
,
.
从定义可以看出，使用Big Oh Notation的过程中，需要求解这3个量：起始点（n0）、倍数（c）和基准函数。关于基准函数，我们一般可以选取简单的对数函数、线性函数等，一个个去套，哪个更合适就用哪个。
除了定义外，Big Oh Notation还有3个数学特性：和（summation）、积（product）以及传递性。
- What can we say about the asymptotic behavior of the sum of
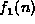and 
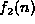? (Theorems 
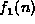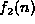and ). - What can we say about the asymptotic behavior of the product of and ? (Theorems and ).
- How are 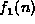and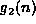
related when 
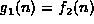? (Theorem ).
2，通过Big Oh Notation的积性质（product），可以直接求出两个多项式相乘后的上界；
3，通过Big Oh Notation的的传递性，一般与和结合使用；
4，多项式的Big Oh Notation，由最高次幂项，其中它的系数要大于0。
In fact, whenever we have a function, which is a polynomial in n, 
we will immediately ``drop'' the less significant terms (i.e., terms involving powers of n which are less than m), as well as the leading coefficient, 
, to write 
.
5，以10为底的对数的Big Oh Notation，参考点击打开链接
三、Tight Big Oh bound
Definition (Tightness) Consider a function f(n)=O(g(n)). If for every function h(n) such that f(n)=O(h(n)) it is also true that g(n)=O(h(n)), then we say that g(n) is a tight asymptotic bound onf(n).
Certain conventions have evolved which concern how big oh expressions are normally written:
- First, it is common practice when writing big oh expressions to drop all but the most significant terms. Thus, instead of
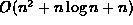we simply write . - Second, it is common practice to drop constant coefficients. Thus, instead of
, we simply write . As a special case of this rule, if the function is a constant, instead of, say O(1024), we simply write O(1).
Of course, in order for a particular big oh expression to be the most useful, we prefer to find a tight asymptotic bound (see Definition ). For example, while it is not wrong to write 
, we prefer to write f(n)=O(n), which is a tight bound.
以上是关于Big Oh Notation的一些约定。同时，学术界也给一些常用的Big Oh expression进行了特意命名，参考点击打开链接