ZOJ 3328 WuXing

题目链接：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3328

题面：

Wu Xing Time Limit: 1 Second       Memory Limit: 32768 KB

Introduction

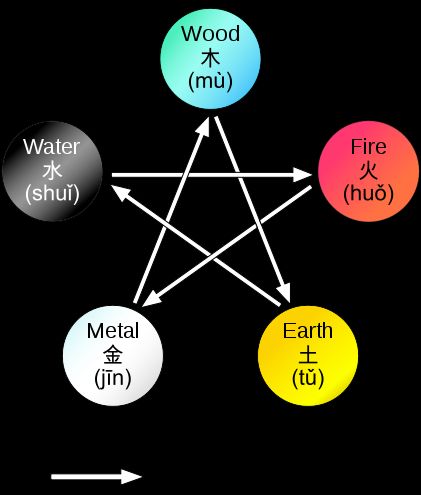
The Wu Xing, or the Five Movements, Five Phases or Five Steps/Stages, are chiefly an ancient mnemonic device, in many traditional Chinese fields.

The doctrine of five phases describes two cycles, a generating or creation cycle, also known as "mother-son", and an overcoming or destruction cycle, also known as "grandfather-nephew", of interactions between the phases.

Generating:

• Wood feeds Fire;
• Fire creates Earth (ash);
• Earth bears Metal;
• Metal carries Water (as in a bucket or tap, or water condenses on metal);
• Water nourishes Wood.

Overcoming:

• Wood parts Earth (such as roots) (or Trees can prevent soil erosion );
• Earth absorbs (or muddies) Water (or Earth dam control the water);
• Water quenches Fire;
• Fire melts Metal;
• Metal chops Wood.

With the two types of interactions in the above graph, any two nodes are connected by an edge.

Problem

In a graph with N nodes, to ensure that any two nodes are connected by at least one edge, how many types of interactions are required at least? Here a type of interaction should have the following properties:

• It can be represented as a set of directed edges in the graph.
• For each type of interaction, there should be one and only one edge starting at each node.
• For each type of interaction, there should be one and only one edge ending at each node.
• The interactions are made up of cycles, i.e. starting from an arbitrary node and following the edges with the same type of interaction, you can always reach the starting node after several steps.

Input

For each test case, there's a line with an integer N (3 <= N < 1,000,000), the number of nodes in the graph.

N  = 0 indicates the end of input.

Output

For each test case, output a line with the number of interactions that are required at least.

Sample Input

5
0

Sample Output

2

Reference

http://en.wikipedia.org/wiki/Wu_Xing

题意：

   用多少种圈关系，可以使任意两边间都可以直接连一条边。

解题：

   一开始看到这种题都是比较晕的吧，仔细读了题之后，发现题目很简单，就是求需要多少种圈关系，可以使得任意两点间都可以连一条边。比如一种关系可以使1个点与另外两个点建立关系。故可得出需要的关系数为n/2。

代码：

#include<iostream>
using namespace std;
int main()
{
	int n;
	while(cin>>n&&n)
	{
		cout<<n/2<<endl;
	}
}