POJ 1556 The Doors (线段相交+Dijkstra)

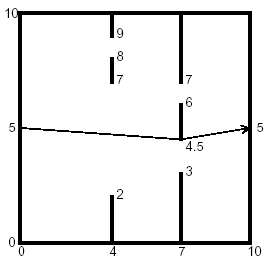
题意：找从起点到终点的最短路径。

题解：可以知道，但凡两点不能直达，则一定是沿着墙边界点走的，这样才能保证路径最短。那么只需要再所有可以直达的点间连上一条边，求一次最短路径。注意判断两线段是否相交应该是判断“严格相交”，即不包含端点。

#include <cmath>
#include <cstdio>
/*
#include <iostream>  //不知道为什么加上这两句就报一些奇怪的错误····
using namespace std; 
*/

#define MAX 500
#define eps 1e-8
#define INF 999999999999
#define zero(x) ( ((x) > 0 ? (x) : -(x)) < eps )

struct Point { double x, y;};
struct Line { Point a, b;};
Point point[MAX];
Line line[MAX];

double dis[MAX], edge[MAX][MAX];
bool vis[MAX];

double xmult ( Point p1, Point p2, Point p0 )  // 叉积
{
	return (p1.x-p0.x)*(p2.y-p0.y) - (p2.x-p0.x)*(p1.y-p0.y);
}

bool oPointosite_side ( Point p1, Point p2, Point l1, Point l2 ) // 判断同侧或者异侧
{
	return xmult(l1,p1,l2) * xmult(l1,p2,l2) < -eps;
}

bool intersect_ex ( Point u1, Point u2, Point v1, Point v2 ) // 判断是否相交
{
	return oPointosite_side(u1,u2,v1,v2) && oPointosite_side(v1,v2,u1,u2);
}

double distance ( Point p1, Point p2 ) // 求两点间的距离
{
	return sqrt((p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y));
}

bool check ( int lnum, Point p1, Point p2 )  // 对于任意两个点i,j，枚举所有的边，若它不与任意边相交，则返回true
{
	for ( int i = 1; i <= lnum; i++ )
	{
		if ( intersect_ex ( p1, p2, line[i].a, line[i].b ) )
			return false;
	}
	return true;
}

void build_map ( int pnum, int lnum )
{
	int i, j;
	for ( i = 0; i < pnum; i++ )
		for ( j = i + 1; j <= pnum; j++ )
			edge[i][j] = edge[j][i] = INF;

	for ( i = 0; i < pnum; i++ )
	{
		for ( j = i + 1; j <= pnum; j++ )
			if ( check ( lnum, point[i], point[j] ) ) // 若 i, j 之间没有墙壁阻挡，则可连一条边
				edge[i][j] = edge[j][i] = distance ( point[i], point[j] );
	}
}

double Dijkstra ( int pnum )
{
	int i, j, k;
	for ( i = 0; i <= pnum; i++ )
	{
		dis[i] = edge[0][i];
		vis[i] = 0;
	}
	vis[0] = true;
	dis[0] = 0;
	for ( i = 1; i <= pnum; i++ )
	{
		double minc = INF;
		for ( j = 0; j <= pnum; j++ )
		{
			if ( ! vis[j] && minc > dis[j] )
			{
				minc = dis[j];
				k = j;
			}
		}
		if ( minc == INF ) break;
		vis[k] = true;
		dis[k] = minc;
		for ( j = 0; j <= pnum; j++ )
		{
			if ( ! vis[j] && dis[j] > dis[k] + edge[k][j] )
				dis[j] = dis[k] + edge[k][j];
		}
	}
	return dis[pnum];
}

int main()
{
	int n;
	while ( scanf("%d",&n) )
	{
		if ( n == -1 ) break;
		double x, y1, y2, y3, y4;
		int i, p = 0, l = 0;
		point[0].x = 0; point[0].y = 5; // 0 为起点

		for ( i = 1; i <= n; i++ )
		{
			scanf("%lf %lf %lf %lf %lf", &x, &y1, &y2, &y3, &y4 );
			l++;
			line[l].a.x = line[l].b.x = x;
			line[l].a.y = 0; line[l].b.y = y1;
			l++;
			line[l].a.x = line[l].b.x = x;
			line[l].a.y = y2; line[l].b.y = y3;
			l++;
			line[l].a.x = line[l].b.x = x;
			line[l].a.y = y4; line[l].b.y = 10;

			p++;
			point[p].x = x; point[p].y = y1;
			p++;
			point[p].x = x; point[p].y = y2;
			p++;
			point[p].x = x; point[p].y = y3;
			p++;
			point[p].x = x; point[p].y = y4;
		}
		p++;
		point[p].x = 10; point[p].y = 5; // p 为终点
		build_map ( p, l );
		double res = Dijkstra ( p );
		printf("%.2lf\n",res);
	}
	return 0;
}