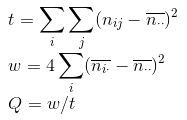R语言与抽样技术学习笔记(Randomize)
R语言与抽样技术学习笔记(Randomize,Jackknife,bootstrap)
尽管二次抽样、重新抽样或者其他的对给定数据重新排序的方法并不能增加数据的信息,但是这些办法往往有助于我们提取信息。今天我们就来详细的讨论一下抽样技术在数据分析中的作用。主要包括随机化检验、Jackknife、bootstrap三个方面的内容。
女士品茶实验与随机化检验
首先我们还是来回顾一下Fisher爵士的女士品茶实验。一种饮品由牛奶与茶混合而成,它的制作工艺可以是先放奶后放茶(这里我们可以称之为奶茶)也可以是先放茶后放奶(这里我们称之为茶奶)。一位女士声称她可以分辨出这个饮品是茶奶还是奶茶。那么我们有办法来检验这位女士所说的话吗? Fisher爵士给出了一个办法:准备8杯饮品,4杯茶奶4杯奶茶,随机排列让该女士一一品鉴,看看该女士的判断是否正确。这个检验合理吗?假设该女士都品尝正确,那么她是随机猜测的概率仅有1/70。由于发生一件1/70的事件还是蛮稀奇的,所以我们有理由相信这个女士是有品鉴能力的。 这里我们关注的重点并非Fisher的显著性检验思想而是随机化安排茶奶与奶茶的想法。这个想法被称为随机性检验。尽管这一想法的根在1935年Fisher的论文中,但广泛的使用却是在Edgington(1995)之后。 我们以一个简单的例子来介绍一下随机化检验的想法。我们考虑两个样本:
我们想要检验这两个样本的均值是否是一样的。我们考虑一个非常粗糙的统计量t=mean(x)-mean(y)。现在我们考虑一个同样观测集构造的不同样本:
也就是我们可以每次用一些y的集合中的元素替换x中的一些元素,或者说我们可以将数据集充分混合,取出n2个元素构成的集合作为y,剩下的作为x。那么我们最终得到{(n1+n2)!}/{(n1)!(n2)!}个数据集,我们对每一个数据集计算一遍我们前面定义的t统计量。如果我们的原假设:两组数据均值一致是对的,那么我们算出的t不应该与充分混合后挑出的“数据集”算出的t有太大的差别。对应的p-value可以利用不同数据集给出的t的经验分布给出,样本太大时,我们也可以用抽样的办法来计算一些子集的t值。 我们来简单的模拟这一过程,假设x是均值为5的正态分布的随机数构成的集合,y是均值为3的指数分布构成的集合,我们来执行这一检验:
x <- rnorm(100, 5) y <- rexp(100, 1/3) t <- mean(x) - mean(y) tvalue <- NULL for (i in 1:10000) { x1 <- sample(union(x, y), length(x), replace = FALSE) y1 <- setdiff(union(x, y), x1) tvalue[i] <- mean(x1) - mean(y1) } (conf <- quantile(tvalue, c(0.025, 0.975)))
## 2.5% 97.5%
## -0.6721 0.6956
我们可以清楚的看到我们原数据集计算出的t值并不在置信区间conf内,我们有足够的理由(在95%的置信水平下)否决我们的原假设,当然我们也可以通过求解t对应的分位数来估计出pvalue的。这里我们没有用到任何分布的信息,这是这个检验的优点,但是检验质量的好坏还是取决于统计量的构造了。
我们来看一个复杂一些的例子,这是一个考虑二维平面上均匀分布的问题。一般在生物均匀分布上很有用处,当然,其他地方也可能用到。我们将问题描述如下:生物学家希望研究一种数目如何在森林中分布的。生物学家先将给定区域的特定树木的位置画了下来,假设有47棵树,它们分布如下:
生物学家认为这些树木的分布是均匀的,没有出现聚类的趋势。那么我们应该怎么去对这个假设做检验呢?许多统计学家对这个问题给出了不同的答案,如Besag,Diggle(1977)提出的Monte Carlo test,当然bootstrap也是可以的,Mead(1974)提出的随机化检验也是解决问题的办法之一。
Mead的想法是这样的:我们将这幅图划分为n个大格,每个大格有划分n个小格。我们可以计算大方格中计数的方差与小方格的计数方差之比。令n_{ij}是在第i个大格中第j个小格中的观测计数。记![]() 为第i个大格的平均数,记
为第i个大格的平均数,记![]() 为总体的平均数,我们将统计量Q定义为:
为总体的平均数,我们将统计量Q定义为:
这里我们将网格数n取为了4.我们将划分显示如图:
这里我们采用随机化检验,即将这16个小格随机排列,得到新的数据集,用同样的办法计算Q,我们有理由相信,在原假设成立下,Q的表现不会过于极端,因为产生极端值(考虑特别极端——Q取到最大,最小值的情况)的可能性也只有1.5857 × 10-8,我们认为这么小概率的事件在这一次不发生。我们这里还是采用抽样的办法来构造置信区间:
A <- data.frame(x = x, y = y) n <- matrix(rep(-1, 16), 4, 4) for (i in 1:4) { k <- -1 + 0.5 * i for (j in 1:4) { h <- -1 + 0.5 * j n[i, j] <- length(A[k - 0.5 <= x & x < k & h - 0.5 <= y & y < h, 1]) } } w <- 4 * ((mean(n[1:2, 1:2]) - mean(n))^2 + (mean(n[3:4, 1:2]) - mean(n))^2 + (mean(n[1:2, 3:4]) - mean(n))^2 + (mean(n[3:4, 3:4]) - mean(n))^2) t <- sum((n - mean(n))^2) (Q <- w/t)
## [1] 0.3348
Qvalue <- NULL n1 <- n for (i in 1:10000) { n <- matrix(sample(n1, 16), 4, 4) w1 <- 4 * ((mean(n[1:2, 1:2]) - mean(n))^2 + (mean(n[3:4, 1:2]) - mean(n))^2 + (mean(n[1:2, 3:4]) - mean(n))^2 + (mean(n[3:4, 3:4]) - mean(n))^2) t1 <- sum((n - mean(n))^2) Qvalue[i] <- w1/t1 } quantile(Qvalue, c(0.025, 0.975))
## 2.5% 97.5%
## 0.02376 0.52484
我们可以清楚的看到,Q=0.3348确实落在了95%的置信区间内,我们不能拒绝原假设,树木的确是均匀分布的。这个确实是这样的,因为这一次的数据并非来自真实,而是我们人为构造的。我通过生成独立同分布的x,y(均服从[-1,1]上的均匀分布)构造的这个例子。现在我们可以看看我人为构造数据的代码了:
set.seed(5000) x <- runif(47, -1, 1) set.seed(500) y <- runif(47, -1, 1)
本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。