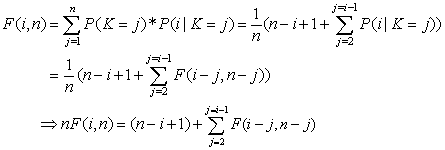【编程之美】金刚坐飞机问题

 题目描述

现在有一架飞机要起飞，乘客们正准备按机票号码（1,2,3...,N）一次排队登机。突然来了一只大猩猩（金刚）。他也有机票，但是他插队第一个登上了飞机，然后随意的选择了一个座位坐下了。根据社会的和谐程度，其他的乘客有两种反应：

1.乘客们都义愤填膺，“既然金刚同志都不守规矩，为什么我要遵守？”他们也随意的找位置坐下，并且坚决不让座位给其他乘客。

2.乘客们虽然感到愤怒，但是还是以“和谐”为重，如果自己的位置没有被占领，就赶紧坐下，如果自己的位置已经被别人（或者金刚同志）占了，就随机的选择另一个位置坐下，就开始闭目养神，不在挪动。

问题：在这两种情况下，第i个乘客（出去金刚同志外）做到自己原机票位置的概率分别是多少？

问题解答

第一问：该问题相当于排序问题，总的排序总数是n个人的全排列为N!，如果第i个人做到第i个位置上，那么其余n-1个人的全排列为(N-1)!,综上所求概率为(N-1)!/N!=1/N。

第二问：《编程之美》讲得比较复杂，没怎么看懂，在网上找了几个博文对该问题的解答，综合一下，这样理解比较容易：

假设：F(i,n)表示在有n个座位的前提下，第i个人恰好做到第i个座位的概率；

P(K=j)表示金刚刚好坐在位置j上的概率；

P(i|K=j)表示在金刚做到位置ｊ的前提下，第ｉ个人恰好做到第ｉ个位置上的概率。

由以上的假设根据全概率公式有：

　　由于金刚坐到每一个位置上的概率是相等的，容易知道Ｐ（Ｋ＝ｊ）＝１／ｎ；

　　接下来我们只需要考虑后一项条件概率的值即可。

　　（１）如果ｊ＝１，则表明金刚坐到第一个位置，则ｉ坐到ｉ位置的概率为１；如果ｊ＞ｉ，前面的人必然按位置坐，所以概率也为１.所以我们只需要考虑１＜ｊ＜ｉ的情况，见下。

　　（２）在１＜ｊ＜ｉ的情况下，即金刚坐在第ｊ（１＜ｊ＜ｉ）个位置上，则ｊ个乘客除非坐在金刚的位置上，否则同样要同样要抢占其他人的座位。这和金刚的行为是相似的（因为金刚除非坐在自己的位置上，否则抢占别人的座位），所以我们可以讲第ｊ个乘客当做新的金刚，此时还剩余ｎ－ｊ个座位，同时把剩余乘客的编号也都减去ｊ，则先前的第ｉ个乘客座位号变为ｉ－ｊ，此问题和原问题相似，只是规模更小，所以该种情况下，条件概率为Ｆ（ｉ－ｊ，ｎ－ｊ）.

　　所以有如下等式：

 　　然后可以从上面的公式推出递推式：F(i,n)=F(i-1,n-1).（笔者验证了一下，公式是对的，但是不会推导，希望有会的网友指点）。

　　有上面的递推公式，我们可以到：nF(i,n)=(n-i+1)+(i-2)F(i,n)，则问题的最终答案为：

　　

参考文献：

1. 《编程之美》P265-P267

2. http://hi.baidu.com/maxint/blog/item/8ac3c49707911f6354fb96e9.html

3. http://blog.sina.com.cn/s/blog_7cd1ba470100rgkz.html

转载自:http://www.cnblogs.com/python27/archive/2012/04/08/2438009.html

人人面试就死在这类似的题目上,哎...