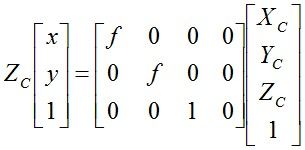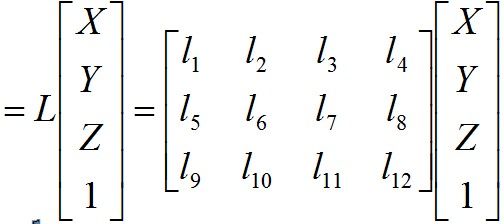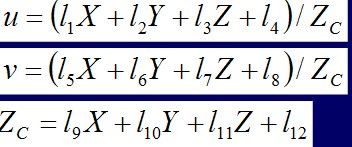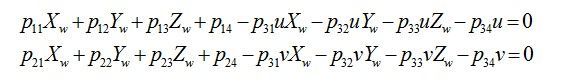双目视觉算法研究(二)相机模型和直接线性法(DLT)
一、相机数学模型
相机模型为以后一切标定算法的关键,只有这边有相当透彻的理解,对以后的标定算法才能有更好的理解。本人研究了好长时间,几乎每天都重复看几遍,最终才会明白其推导过程。
我觉得首先我们要理解相机模型中的四个平面坐标系的关系:像素平面坐标系(u,v)、像平面坐标系(图像物理坐标第(x,y)、相机坐标系(Xc,Yc,Zc)和世界坐标系(Xw,Yw,Zw),在每一篇介绍相机模型的文章中都有介绍。
我刚开始理解时,看着那一堆的公式十分的头晕,我相信很多初学者和我一样,但仔细想想,只不过是,我们假设了一些参数,使四个坐标系之间的坐标联系起来,这样我们就可以从拍摄的图片上一个点坐标一路反推出世界中的那个点的坐标,这样就达到了我们的目的,三维重建。而那些我们假设的参数,就是我们要标定的内外参数。
1、像素坐标与像平面坐标系之间的关系
确定他们的关系之前,我们可以假设每一个像素在u轴和v轴方向上的物理尺寸为dx和dy。仔细看下他们的模型可以推出以下公式(这个还是比较好理解的):
公式1
解释:1、dx,dy,u0,v0其实都是我们假设出来的参数,dxdy表示感光芯片上像素的实际大小,是连接像素坐标系和真实尺寸坐标系的,u0,v0是图像平面中心,最终是要我们求的内外参数。
得出这个公式后我们可以运用线性代数的知识把方程用矩阵形式表示:
公式2
当然我们也可以用另一种矩阵形式表示:
公式3
2、相机坐标系与世界坐标系之间的关系
这两个坐标系之间的关系我们可以旋转矩阵R和平移矩阵T来得到以下关系:
公式4
解释:1、 在这个公式中,R为3*3矩阵,T为3*1,0为(0,0,0),简化用Lw表示后为4*4矩阵。
3、成像投影关系(相机坐标系与像平面坐标系)
在相机模型中我们可以得到以下公式:
公式5
解释:1、
同样我们用矩阵形式表示:
公式6
4、得到公式
而我们可以将以上公式综合一下就可以得到:
乘开用方程表示:
把Zc代替可得到以下公式:
解释:1、式中:L1,L2,…,L11是11个与u0,v0,f,Kx,Ky,U,X,J及XS,YS,ZS有关的系数;确定了像机的成像特性。x0,y0,f称为摄像机内方位元,U,X,J与XS,YS,ZS称为摄像机外方位元。若已知6个以上空间点(X i,Y i,Z i)及其像坐标(u i,v i)就可由式上式解出L1,L2,…,L11;从而得到像机参数。若已知两部以上像机的参数L1,L2,…,L11;根据空间点在各摄像机的像坐标(x j,y j),由上式就可解算出空间坐标(X,Y,Z)。确定L1,L2,…,L11的过程称为标定,由(xj,yj)解算(X,Y,Z)的过程称为重构。
由于公式是复制得,以下用P代替:
移项可得:
解释:1、由上可见,由空间6个以上的已知点与它们的图像点坐标就可以得到P矩阵。在一般的标定工作中,靶标上有数十个已知特征点,使方程的个数大大超过未知数的个数,从而用最小二乘法求解以降低误差造成的影响。
2、当标定点有N个时,就意味着上述方程有2N个,此时我们可以用矩阵把这2N个方程表示出来,该公式为:
其中L为:
A为:
U为:
这个公式大家可以写出来,这样就比较好看了,列出来以后可以看出P34对其他值是没有影响的,因此令P34=1。
上面说了,在2N个点时,我们可以通过最小二乘法使结果更加精确,其结果为:
公式 解释:1、因为在实际坐标与图像坐标为已知,所以A和U是已知的,所以可求出L。
2、P34为1,所以所求出的L为P11到P33.
这样所有的P我们都求出来了,这就又回到了上式中,我们用P参数把内外参数的公式代替方便求解,我们可以通过P参数来反推出内外参数,由于这部分比较好理解,就不写了,粘贴公式太麻烦了。