poj 1681 Painter's Problem 【高斯消元 + 状压枚举自由变元】
Painter's Problem
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 5075 | Accepted: 2458 |
Description
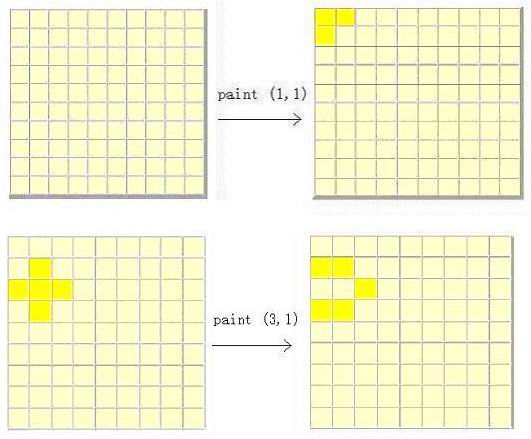
There is a square wall which is made of n*n small square bricks. Some bricks are white while some bricks are yellow. Bob is a painter and he wants to paint all the bricks yellow. But there is something wrong with Bob's brush. Once he uses this brush to paint brick (i, j), the bricks at (i, j), (i-1, j), (i+1, j), (i, j-1) and (i, j+1) all change their color. Your task is to find the minimum number of bricks Bob should paint in order to make all the bricks yellow.

Input
The first line contains a single integer t (1 <= t <= 20) that indicates the number of test cases. Then follow the t cases. Each test case begins with a line contains an integer n (1 <= n <= 15), representing the size of wall. The next n lines represent the original wall. Each line contains n characters. The j-th character of the i-th line figures out the color of brick at position (i, j). We use a 'w' to express a white brick while a 'y' to express a yellow brick.
Output
For each case, output a line contains the minimum number of bricks Bob should paint. If Bob can't paint all the bricks yellow, print 'inf'.
Sample Input
2 3 yyy yyy yyy 5 wwwww wwwww wwwww wwwww wwwww
Sample Output
015
题意:给你一个n*n的矩阵,每个位置对应一个字符,y代表该位置是黄色的,w代表该位置是白色的。若你选择覆盖位置(i, j),则(i, j)位置的颜色会由黄变白(或者由白变黄),且该效应会影响到(i-1, j)、(i, j-1)、(i+1, j)、(i, j+1)这些位置。现在让你选择最少的覆盖位置使得矩阵上所有位置均为黄色,若可以达到目标输出覆盖位置的最少个数,若不能达到目标输出inf。
思路:n*n个方程,n*n个变元,求解自由变元。然后状态压缩枚举自由变元,维护最小值。
方程很好列的,初始状态和结束状态题目已给出。
——(相关位置)*1 ^ (非相关位置)*0 = 初始状态^结束状态
AC代码:
#include <cstdio> #include <cstring> #include <algorithm> #define MAXN 300 #define INF 0x3f3f3f3f using namespace std; char str[MAXN][MAXN]; int a[MAXN][MAXN]; bool free_x[MAXN];//标记是否是自由变元 int free_rec[MAXN];//记录自由变元 int x[MAXN];//解集 int equ, var; int n; void init_a() { scanf("%d", &n); equ = var = n*n; memset(a, 0, sizeof(a)); for(int i = 0; i < n; i++) { scanf("%s", str[i]); for(int j = 0; j < n; j++) { int num = i*n+j; if(str[i][j] == 'y') a[num][var] = 0^0; else a[num][var] = 0^1; a[num][num] = 1; if(i > 0) a[num][num-n] = 1; if(j > 0) a[num][num-1] = 1; if(i < n-1) a[num][num+n] = 1; if(j < n-1) a[num][num+1] = 1; } } } int Gauss() { int max_r, k; int col = 0; int num = 0;//自由变元编号 for(k = 0; k < equ && col < var; k++, col++) { max_r = k; for(int i = k+1; i < equ; i++) if(a[i][col] > a[max_r][col]) max_r = i; if(max_r != k) for(int i = col; i < var+1; i++) swap(a[k][i], a[max_r][i]); if(a[k][col] == 0) { k--; free_rec[num++] = col;//记录自由变元 continue; } for(int i = k+1; i < equ; i++) if(a[i][col] != 0) for(int j = col; j < var+1; j++) a[i][j] ^= a[k][j]; } for(int i = k+1; i < equ; i++) if(a[i][col] != 0)//在k+1 ~ equ-1行的col列出现非0的情况 return -1;//无解 if(k < var) return var - k;//返回自由变元数目 return 0; } void solve(int S) { int state = (1<<S); int ans = INF; for(int i = 0; i < state; i++)//妆压 枚举所有状态 { int cnt = 0; for(int j = 0; j < S; j++)//枚举自由变元 并确定自由变元的解 { if((1<<j) & i) { cnt++; x[free_rec[j]] = 1; } else x[free_rec[j]] = 0; } //在0 ~ k-1行形成上三角矩阵 而00...0行只会出现在k ~ equ-1 for(int j = var-S-1; j >= 0; j--) { int temp = a[j][var];//该行对应方程 最终结果 //由最终结果推导 for(int l = j+1; l < var; l++)//根据已经确定的变元来求解该变元 if(a[j][l]) temp ^= x[l]; x[j] = temp;//该变元的解 cnt += x[j] ? 1 : 0; } ans = min(ans, cnt); } printf("%d\n", ans); } int main() { int t; scanf("%d", &t); while(t--) { init_a(); int free_num = Gauss(); if(free_num == -1) printf("inf\n"); else solve(free_num); } return 0; }