直线生成算法

直线生成算法http://blog.csdn.net/orbit/article/details/7185982

在欧氏几何空间中，平面方程就是一个三元一次方程，直线就是两个非平行平面的交线，所以直线方程就是两个三元一次方程组联立。但是在平面解析几何中，直线的方程就简单的多了。平面几何中直线方程有多种形式，一般式直线方程可用于描述所有直线：

 

Ax+By+C = 0  （A、B不同时为0）

 

当知道直线上一点坐标（X₀，Y₀）和直线的斜率K存在时，可以用点斜式方程：

 

Y-Y₀ = K(X – X₀) （当K不存在时，直线方程简化成X = X₀）

 

当知道直线上的两个点(X₀,Y₀)和(X₁,Y₁)时，还可以用两点式方程描述直线：

 

 

除了这三种形式的直线方程外，直线方程还有截距式、斜截式等多种形式。

 

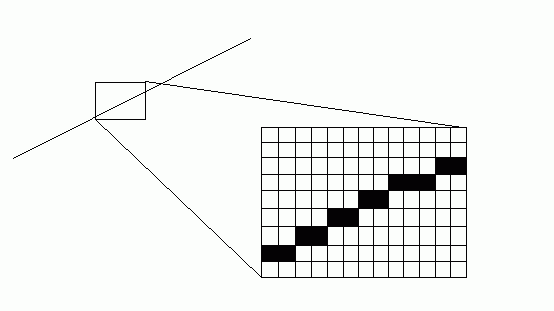
        在数学范畴内的直线是由没有宽度的点组成的集合，但是在计算机图形学的范畴内，所有的图形包括直线都是输出或显示在点阵设备上的，被成为点阵图形或光栅图形。以显示器为例，现实中常见的显示器（包括CRT显示器和液晶显示器）都可以看成由各种颜色和灰度值的像素点组成的象素矩阵，这些点是有大小的，而且位置固定，因此只能近似的显示各种图形。图（1）就是对这种情况的一种夸张的放大：

 图（1）直线在点阵设备上的表现形式

 

        计算机图形学中的直线生成算法，其实包含了两层意思，一层是在解析几何空间中根据坐标构造出平面直线，另一层就是在光栅显示器之类的点阵设备上输出一个最逼近于图形的象素直线，而这就是常说的光栅图形扫描转换。本文就是介绍几种常见的直线生成的光栅扫描转换算法，包括数值微分法（DDA法）、Bresenham算法、对称直线生成算法以及两步算法。

 

数值微分法（DDA法）

        数值微分画线算法（DDA）法是直线生成算法中最简单的一种，它是一种单步直线生成算法。它的算法是这样的：首先根据直线的斜率确定是以X方向步进还是以Y方向步进，然后沿着步进方向每步进一个点（象素），就沿另一个坐标变量k，k是直线的斜率，因为是对点阵设备输出的，所以需要对每次计算出来的一对坐标进行圆整。

        具体算法的实现，除了判断是按照X方向还是按照Y方向步进之外，还要考虑直线的方向，也就是起点和终点的关系。下面就是一个支持任意直线方向的数值微分画线算法实例：

12 void DDA_Line(int x1, int y1, int x2, int y2) 13 { 14     double k,dx,dy,x,y,xend,yend; 15  16     dx = x2 - x1; 17     dy = y2 - y1; 18     if(fabs(dx) >= fabs(dy)) 19     { 20         k = dy / dx; 21         if(dx > 0) 22         { 23             x = x1; 24             y = y1; 25             xend = x2; 26         } 27         else 28         { 29             x = x2; 30             y = y2; 31             xend = x1; 32         } 33         while(x <= xend) 34         {     35             SetDevicePixel((int)x, ROUND_INT(y)); 36             y = y + k; 37             x = x + 1; 38         } 39  40     } 41     else 42     { 43         k = dx / dy; 44         if(dy > 0) 45         { 46             x = x1; 47             y = y1; 48             yend = y2; 49         } 50         else 51         { 52             x = x2; 53             y = y2; 54             yend = y1; 55         } 56         while(y <= yend) 57         {     58             SetDevicePixel(ROUND_INT(x), (int)y); 59             x = x + k; 60             y = y + 1; 61         } 62     } 63 }

数值微分法（DDA法）产生的直线比较精确，而且逻辑简单，易于用硬件实现，但是步进量x，y和k必须用浮点数表示，每一步都要对x或y进行四舍五入后取整，不利于光栅化或点阵输出。

 

Bresenham算法

        Bresenham算法由Bresenham在1965年提出的一种单步直线生成算法，是计算机图形学领域使用最广泛的直线扫描转换算法。Bresenham算法的基本原理就是将光栅设备的各行各列象素中心连接起来构造一组虚拟网格线。按直线从起点到终点的顺序计算直线与各垂直方向网格线的交点，然后确定该列象素中与此交点最近的象素。

 

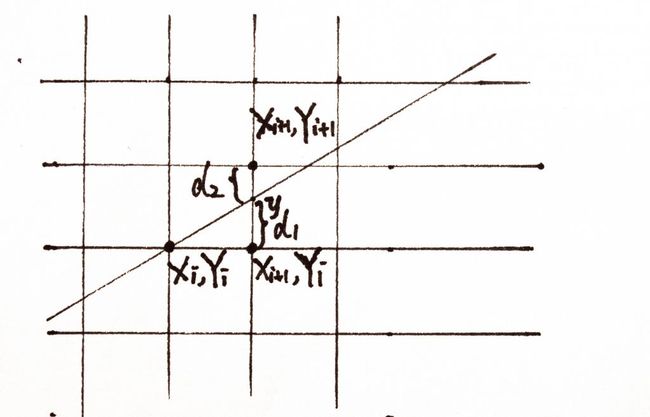
图（2）直线Bresenham算法示意图

 

        图（2）就展示了这样一组网格线，每个交点就代表点阵设备上的一个象素点，现在就以图（2）为例介绍一下Bresenham算法。当算法从一个点（X_i，Y_i）沿着X方向向前步进到X_i+1时，Y方向的下一个位置只可能是Y_i和Y_i+1两种情况，到底是Y_i还是Y_i+1取决于它们与精确值y的距离d1和d2哪个更小。

d1 = y - Y_i                                  （等式 1）

d2 = Y_i+1 - y                                （等式 2）

当d1-d2 > 0时，Y方向的下一个位置将是Y_i+1，否则就是Y_i。由此可见，Bresenham算法其实和数值微分算法原理是一样的，差别在于Bresenham算法中确定Y方向下一个点的位置的判断条件的计算方式不一样。现在就来分析一下这个判断条件的计算方法，已知直线的斜率k和在y轴的截距b，可推导出X_i+1位置的精确值y如下：

y = k X_i+1 + b                                 （等式 3）

 

将等式 1-3带入d1-d2，可得到等式4：

的

d1-d2 = 2k X_i+1 - Y_i - Y_i+1 + 2b                    （等式 4）

 

有因为根据图（2）条件，k = dy / dx，Y_i+1 = Y_i + 1，X_i+1 =  X_i + 1，将此三个关系带入等式4，同时在等式两边乘以dx，整理后可得到等式5：

dx(d1 – d2) = 2dyX_i + 2dy - 2dxY_i + dx(2b - 1)       （等式 5）

 

另p_i = dx(d1 – d2)，则：

p_i = 2dyX_i + 2dy - 2dxY_i + dx(2b - 1)

 

因为图（2）的示例dx是大于0的值，因此p_i的符号与(d1 – d2)一致，现在将初始条件带入可得到最初的第一个判断条件p₁：

p₁ = 2dy – dx

 

根据X_i+1与X_i，以及Y_i+1与Y_i的关系，可以推出p_i的递推关系：

p_i+1 = p_i + 2dy - 2dx(y_i+1 - y_i)

由于y_i+1可能是y_i，也可能是y_i + 1，因此，p_i+1就可能是以下两种可能，并且和y_i的取值是对应的：

p_i+1 = p_i + 2dy    （Y方向保持原值）

或

p_i+1 = p_i + 2(dy – dx)  （Y方向向前步进1）

 

根据上面的推导，当x2 > x1，y2 > y1时Bresenham直线生成算法的计算过程如下：

1、画点(x1,   y1);  计算误差初值p1=2dy-dx；    
2、求直线的下一点位置：    
   X_i+1 = X_i+1；    
   如果 p_i > 0   则Y_i+1 = Y_i + 1；   
   否则Y_i+1 = Y_i；    
   画点(X_i+1, Y_i+1 )；      
3、求下一个误差p_i+1；     
  如果  pi>0   则p_i+1 = p_i+2(dy – dx);    
  否则p_i+1 = p_i+2dy；    
4、如果没有结束，则转到步骤2；否则结束算法。

 

下面就给出针对上面推导出的算法源代码（只支持 x2 > x1，y2 > y1的情况）：

319 void Bresenham_Line(int x1, int y1, int x2, int y2) 320 { 321     int dx = abs(x2 - x1);   322     int dy = abs(y2 - y1);   323     int p = 2 * dy - dx;   324     int x = x1;   325     int y = y1; 326  327     while(x <= x2) 328     {   329         SetDevicePixel(x, y);   330         x++;   331         if(p<0)   332             p += 2 * dy;   333         else 334         {   335             p += 2 * (dy - dx);   336             y += 1;   337         }   338     }   339 }

上面的代码只是演示计算过程，真正实用的代码要支持各种方向的直线生成，这就要考虑斜率为负值的情况以及x1 > x2的情况，另外，循环中的两次乘法运算可以在循环外计算出来，不必每次都计算。要支持各种方向的直线生成其实也很简单，就是通过坐标交换，使之符合上面演示算法的要求即可，下面就是一个实用的，支持各种方向的直线生成的Bresenham算法：

 

164 void Bresenham_Line(int x1, int y1, int x2, int y2) 165 { 166     int dx,dy,p,const1,const2,x,y,inc; 167  168     int steep = (abs(y2 - y1) > abs(x2 - x1)) ? 1 : 0; 169     if(steep == 1) 170     { 171         SwapInt(&x1, &y1); 172         SwapInt(&x2, &y2); 173     } 174     if(x1 > x2) 175     { 176         SwapInt(&x1, &x2); 177         SwapInt(&y1, &y2); 178     } 179     dx = abs(x2 - x1);   180     dy = abs(y2 - y1);   181     p = 2 * dy - dx;   182     const1 = 2 * dy;  183     const2 = 2 * (dy - dx); 184     x = x1;   185     y = y1; 186  187     inc = (y1 < y2) ? 1 : -1; 188     while(x <= x2) 189     {   190         if(steep == 1) 191             SetDevicePixel(y, x);   192         else 193             SetDevicePixel(x, y);   194         x++;   195         if(p<0)   196             p += const1;   197         else 198         {   199             p += const2;   200             y += inc;   201         }   202     }   203 }

        Bresenham算法只实用整数计算，少量的乘法运算都可以通过移位来避免，因此计算量少，效率高，

 

对称直线生成算法(改进的Bresenham算法)

        直线段有个特性，那就是直线段相对于中心点是两边对称的。因此可以利用这个对称性，对其它单步直线生成算法进行改进，使得每进行一次判断或相关计算可以生成相对于直线中点的两个对称点。如此以来，直线就由两端向中间生成。从理论上讲，这个改进可以应用于任何一种单步直线生成算法，本例就只是对Bresenham算法进行改进。

        改进主要集中在以下几点，首先是循环区间，由[x1, x2]修改成[x1, half]，half是区间[x1, x2]的中点。其次是X轴的步进方向改成双向，最后是Y方向的值要对称修改，除此之外，算法整体结构不变，下面就是改进后的代码：

205 void Sym_Bresenham_Line(int x1, int y1, int x2, int y2) 206 { 207     int dx,dy,p,const1,const2,xs,ys,xe,ye,half,inc; 208  209     int steep = (abs(y2 - y1) > abs(x2 - x1)) ? 1 : 0; 210     if(steep == 1) 211     { 212         SwapInt(&x1, &y1); 213         SwapInt(&x2, &y2); 214     } 215     if(x1 > x2) 216     { 217         SwapInt(&x1, &x2); 218         SwapInt(&y1, &y2); 219     } 220     dx = x2 - x1;   221     dy = abs(y2 - y1);   222     p = 2 * dy - dx;   223     const1 = 2 * dy;  224     const2 = 2 * (dy - dx); 225     xs = x1;   226     ys = y1; 227     xe = x2; 228     ye = y2; 229     half = (dx + 1) / 2; 230     inc = (y1 < y2) ? 1 : -1; 231     while(xs <= half) 232     {   233         if(steep == 1) 234         { 235             SetDevicePixel(ys, xs); 236             SetDevicePixel(ye, xe); 237         } 238         else 239         { 240             SetDevicePixel(xs, ys); 241             SetDevicePixel(xe, ye); 242         } 243         xs++;  244         xe--; 245         if(p<0)   246             p += const1;   247         else 248         {   249             p += const2;   250             ys += inc;   251             ye -= inc;   252         }   253     }   254 }

两步算法

        两步算法是在生成直线的过程中，每次判断都生成两个点的直线生成算法。上一节介绍的对称直线生成方法也是每次生成两个点，但是它和两步算法的区别就是对称方法的计算和判断是从线段的两端向中点进行，而两步算法是沿着一个方向，一次生成两个点。

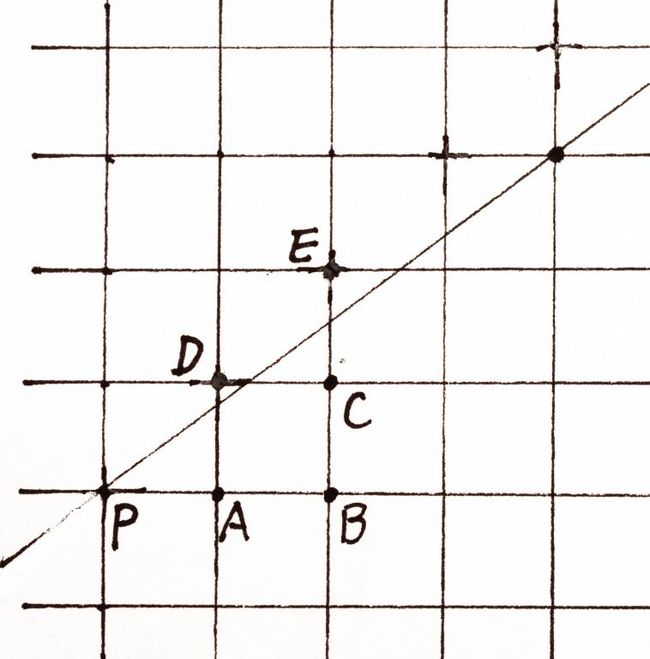
        当斜率k满足条件0≤k＜1时，假如当前点P已经确定，如图（3）所示，则P之后的连续两个点只可能是四种情况：AB，AC，DC和DE，两步算法设立决策量e作为判断标志，e的初始值是4dy – dx，其中：

dy = y2 – y1

dx = x2 – x1。

 

图（3）直线两步算法示意图

 

为简单起见，先考虑dy > dx > 0这种情况。当e > 2dx时，P后两个点将会是DE组合，此时e的增量是4dy – 4dx。当dx < e < 2dx时，P后的两个点将会是DC组合，此时e的增量是4dy – 2dx.。当0 < e < dx时，P后的两个点将会是AC组合，此时e的增量是4dy – 2dx.。当e < 0时，P后的两个点将会是AB组合，此时e的增量是4dy。综合以上描述，当斜率k满足条件0≤k＜1，且dy > dx > 0这种情况下，两步算法可以这样实现：

 

257 void Double_Step_Line(int x1, int y1, int x2, int y2) 258 { 259     int dx = x2 - x1; 260     int dy = y2 - y1; 261     int e = dy * 4 - dx; 262     int x = x1; 263     int y = y1; 264  265     SetDevicePixel(x, y); 266  267     while(x < x2) 268     {   269         if (e > dx) 270         { 271             if (e > ( 2 * dx)) 272             { 273                 e += 4 * (dy - dx); 274                 x++; 275                 y++; 276                 SetDevicePixel(x, y); 277                 x++; 278                 y++; 279                 SetDevicePixel(x, y); 280             } 281             else 282             { 283                 e += (4 *dy - 2 * dx); 284                 x++; 285                 y++; 286                 SetDevicePixel(x, y); 287                 x++; 288                 SetDevicePixel(x, y); 289             } 290         } 291         else 292         { 293             if (e > 0) 294             { 295                 e += (4 * dy - 2 * dx); 296                 x++; 297                 SetDevicePixel(x, y); 298                 x++; 299                 y++; 300                 SetDevicePixel(x, y); 301             } 302             else 303             { 304                 x++; 305                 SetDevicePixel(x, y); 306                 x++; 307                 SetDevicePixel(x, y); 308                 e += 4 * dy;     309             } 310         } 311     } 312 }

以上函数除了只支持一个方向的直线生成之外，还有其它不完善的地方，比如没有判断最后一个点是否会越界，大量出现的乘法计算可以用移位处理等等。仿照Bresenham算法一节介绍的方法，很容易将其扩展为支持8个方向的直线生成，因为代码比较长，这里就不列出代码了。

 

总结

        除了以上介绍的几种直线生成算法，还有很多其它的直线光栅扫描转换算法，比如三步算法、四步算法、中点划线法等等，还有人将三步算法结合前面介绍的对称法提出了一种可以一次画六个点的直线生成算法，这里就不多介绍了，有兴趣的读者可以找计算机图形学的相关资料来了解具体的内容。

        本文介绍的几种直线生成算法中，DDA算法最简单，但是因为有多次浮点数乘法和除法运算，以及浮点数圆整运算，效率比较低。Bresenham算法中的整数乘法计算都可以用移位代替，主要运算都采用了整数加法和减法运算，因此效率比较高，各种各样变形的Bresenham算法在计算机图形软件中得到了广泛的应用。理论上讲，两步算法以及四步算法效率应该更高一些，但是这两种算法需要做比较多的准备工作，且多是乘法和除法运算，因此在生成比较短的直线时，效率反而不如Bresenham算法。