POJ3468--A Simple Problem with Integers(成段更新)
题目大意:给出一个数列,可以进行两种操作,1、给任意一个区间中的每个数增加x,2、求任意一个区间的区间和
分析:用线段树求解。成段更新。(参考了郭炜老师的讲义)
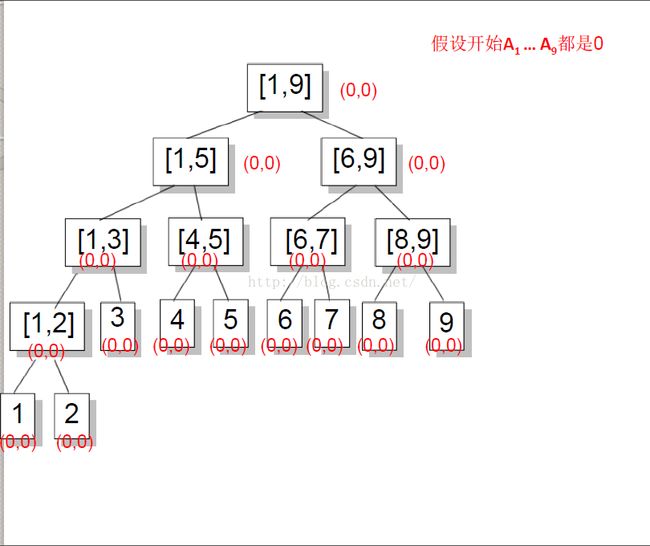
这个题目,首先,要考虑节点里存哪些信息。假设节点里只存sum的话,每次更新都要更新到叶子节点,时间复杂度为O(nlogn),而本题的n以及操作次数均为100000,必然会造成TLE。
一个变量不够怎么办?想到的自然就是增加一个变量。原先的sum变量肯定是要保留的,但是含义稍微变化了,此时的sum表示区间原先的和,即还没有加上现在的增量。增加的inc变量,表示区间中每个数的增量。
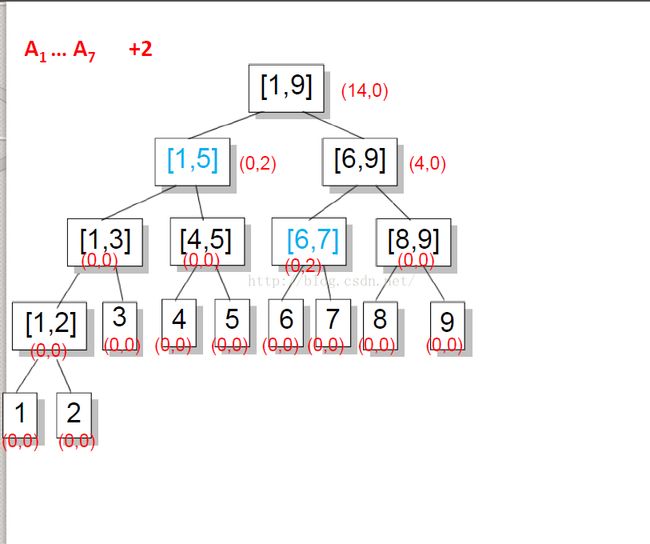
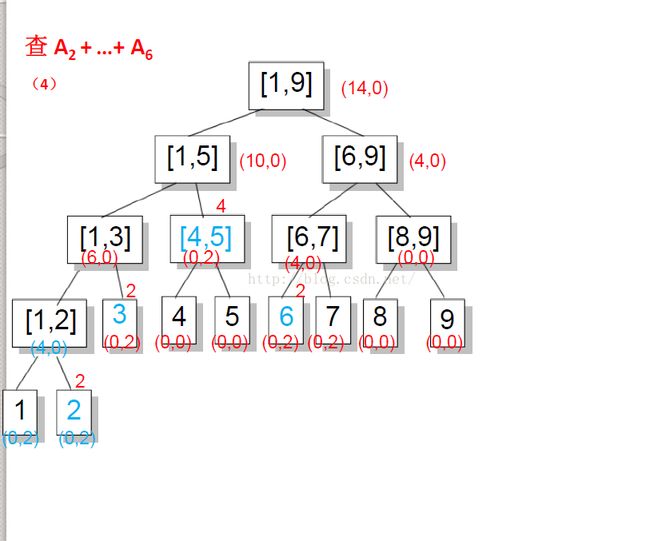
1、进行增加操作时,如果正好覆盖一个区间,那么就只更新inc的值,并return。否则只更新sum,并将inc的值传下去。时间复杂度O(logn)。
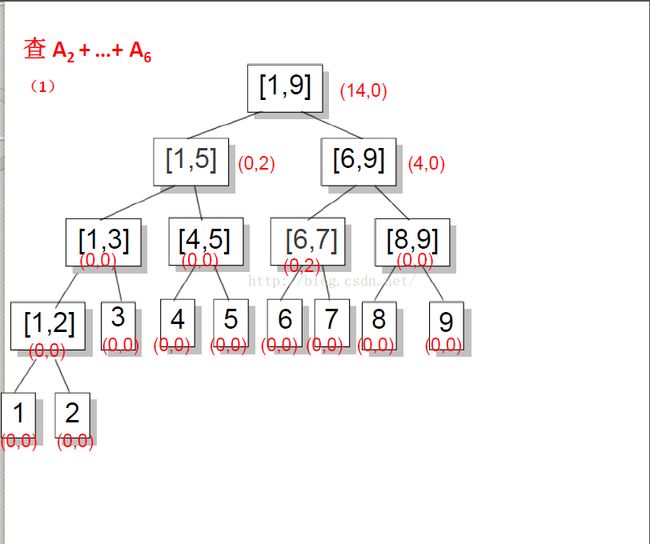
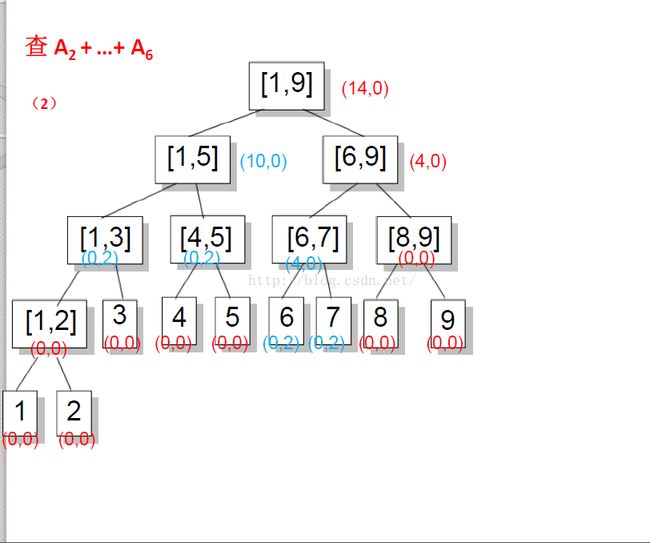
2、进行求和操作时,如果正好覆盖一个区间,那么就加上当前区间的sum值,并return。否则加上(inc * 进行操作的区间长度),并且更新当前区间的sum(即加上(inc * 进行操作的区间长度)),再将inc清零,然后,继续往下查询。时间复杂度(logn)。这一段了的sum都表示节点里的sum,并不是我们需要求的和。
最后,这题大家要特别注意,差不多把所有读入和输出的变量都改为long long,WA了好几发,就只是因为这个原因。。
代码:
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 100000+10;
struct Node {
int l, r;
long long sum;
long long inc;
int Mid(){return (l+r)/2;}
};
Node tree[3*maxn];
long long n, q;
long long sum;
void Build(int root, int l, int r) {
tree[root].l = l;
tree[root].r = r;
tree[root].sum = 0;
tree[root].inc = 0;
if(l != r) {
Build(2*root+1, l, (l+r)/2);
Build(2*root+2, (l+r)/2+1, r);
}
}
void Insert(int root, int i, long long v) {
if(tree[root].l == tree[root].r) {
tree[root].sum = v;
return;
}
tree[root].sum += v;
if(i <= tree[root].Mid())
Insert(2*root+1, i, v);
else
Insert(2*root+2, i, v);
}
void Add(int root, int l, int r, long long x) {
if(tree[root].l == l && tree[root].r == r) {
tree[root].inc += x;
return;
}
tree[root].sum += (r-l+1)*x;
if(r <= tree[root].Mid()) {
Add(2*root+1, l, r, x);
}
else if(l > tree[root].Mid()) {
Add(2*root+2, l, r, x);
}
else {
Add(2*root+1, l, tree[root].Mid(), x);
Add(2*root+2, tree[root].Mid()+1, r, x);
}
}
void Query(int root, int l, int r) {
if(tree[root].l == l && tree[root].r == r) {
sum += tree[root].sum+(r-l+1)*tree[root].inc;
return;
}
tree[root].sum += (tree[root].r-tree[root].l+1)*tree[root].inc;
tree[2*root+1].inc += tree[root].inc;
tree[2*root+2].inc += tree[root].inc;
tree[root].inc = 0;
if(r <= tree[root].Mid()) {
Query(2*root+1, l, r);
}
else if(l > tree[root].Mid()) {
Query(2*root+2, l, r);
}
else {
Query(2*root+1, l, tree[root].Mid());
Query(2*root+2, tree[root].Mid()+1, r);
}
}
int main() {
scanf("%I64d%I64d", &n, &q);
long long x;
Build(0, 1, n);
for(int i = 1; i <= n; i++) {
scanf("%I64d", &x);
Insert(0, i, x);
}
while(q--) {
sum = 0;
char ch[10];
scanf("%s", ch);
if(ch[0] == 'C') {
int a, b;
long long c;
scanf("%d%d%I64d", &a, &b, &c);
Add(0, a, b, c);
}
else {
int a, b;
scanf("%d%d", &a, &b);
Query(0, a, b);
printf("%I64d\n", sum);
}
}
return 0;
}