图之AVO拓扑排序

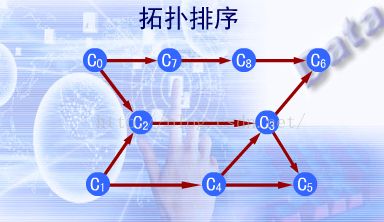
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若<u，v> ∈E(G)，则u在线性序列中出现在v之前。
   　通常，这样的线性序列称为满足拓扑次序(TopoiSicai Order)的序列，简称拓扑序列。将顶点表示活动，有向边表示活动之间的先后关系：即活动u的完成是活动v的开始条件，则在u,v之间存在有向边<u,v>；若从u出发可以到v，则u是v前驱，v是u后继。这样的有向无回图称作AOV网。
注意：
   　①若将图中顶点按拓扑次序排成一行，则图中所有的有向边均是从左指向右的。

   　②若图中存在有向环，则不可能使顶点满足拓扑次序。

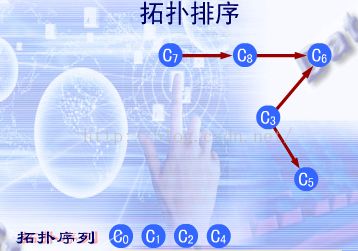
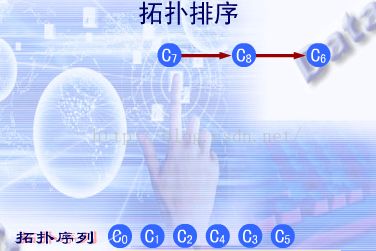
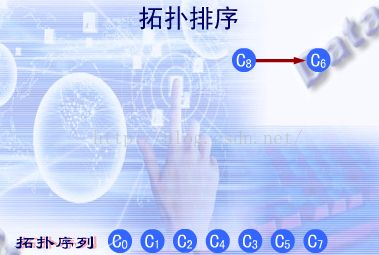
拓扑排序过程描述如下：

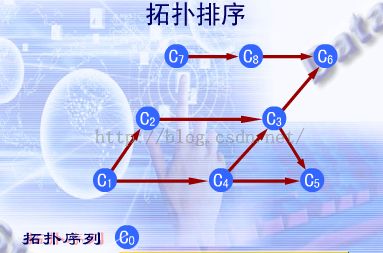
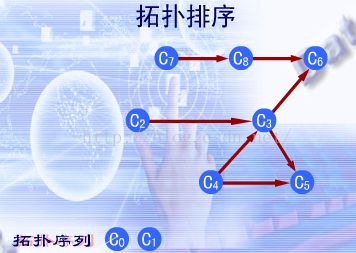
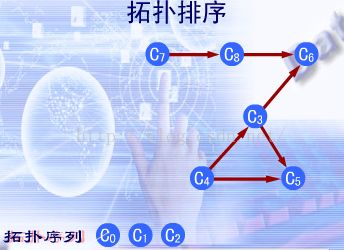
1 .从有向图中选择一个没有前驱即入度为0的顶点并且输出；

2 .从网中删除该 顶点，并且删除以该顶点为始点的全部有向边；

3 .重复上述，直到AVO网络中不再有入度为0的顶点。

顺序如下：

首先生成一个有向无环图：

#include<iostream>
#include<stdlib.h>
#define M 4
//AOV和拓扑排序
struct enode{
int adjvexs;
enode *next;};
struct vnode
{
 int data;
 int count;//入度数目，专为AOV
 enode *first;
};
struct alist{
int e;
int v;
vnode adjvex[M];};
//创建AOV
void create_adjlist_aov(alist*&g,int a[][M],int n){
int i,j;
enode *p;
g=(alist*)malloc(sizeof(alist));
g->v=n;
g->e=0;
for(i=0;i<n;i++)
{  g->adjvex[i].data=i;
    g->adjvex[i].count=0;
    g->adjvex[i].first=NULL;
   for(j=n-1;j>=0;j--)
   {   if(a[i][j]!=0)
       {p=(enode*)malloc(sizeof(enode));
        p->adjvexs=j;
       p->next=g->adjvex[i].first;
       g->adjvex[i].first=p;
       g->e++;}
       if(a[j][i]!=0){g->adjvex[i].count++;}
   }
  }
}
//输出AOV
void dis_aov(alist*g){
enode *p;
int i;
for(i=0;i<g->v;i++)
 {cout<<"与顶点"<<g->adjvex[i].data<<"其入度数"<<g->adjvex[i].count<<
     "以及相邻情况:"<<endl;
p=g->adjvex[i].first;
while(p){cout<<g->adjvex[p->adjvexs].data<<" ";p=p->next;}
cout<<endl;}
}

然后拓扑排序：

利用棧产生：

//拓扑排序,当排成功时返回1并将结果存到topo数组
int Topo_sort(alist*g,int topo[]){
int q[M*M];
int top=-1;
int i,j;
int k=0;
enode *p;
for(i=0;i<g->v;i++)
{ if(g->adjvex[i].count==0){top++;q[top]=i;}
}
while(top>-1){
i=q[top];
top--;
topo[k++];
p=g->adjvex[i].first;
while(p){
    j=p->adjvexs;
    g->adjvex[j].count--;
    if(g->adjvex[j].count==0){top++;q[top]=j;}
    p=p->next; }
}
if(k<g->v)return -1;
else return 1;
}

利用ＤＦＳ遍历产生逆向拓扑排序：

//DFS产生拓扑排序
int visit[M2]={0};//对顶点未访问
int again[M2]={0};//对顶点未搜索完
int topo[M2]={-1,-1,-1,-1,-1,-1};
int f=1;
int k=0;
void dfs_topo(alist*g,int v){
enode *p;
int ff=0;
visit[v]=1;
again[v]=0;
cout<<v<<endl;
p=g->adjvex[v].first;
while(p){
  if(visit[p->adjvexs]==1&&again[p->adjvexs]==0)f=0;
  else if(visit[p->adjvexs]==0){dfs_topo(g,p->adjvexs);again[p->adjvexs]=1;
  }
  p=p->next;
}
topo[k++]=v;
}
int topo_sort(alist*g){
    int i=0;
    while(f==1&&i<g->v){
    if(visit[i]==0)
    dfs_topo(g,i);
    i++;
    }
if(f==1){
for(i=0;i<M2;i++)
    cout<<topo[i]<<" ";
 return 1;}
else return 0;
}