poj 1222 EXTENDED LIGHTS OUT 增广矩阵消元法

EXTENDED LIGHTS OUT

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 8682		Accepted: 5624

Description

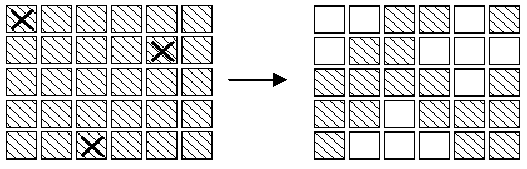
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right. 

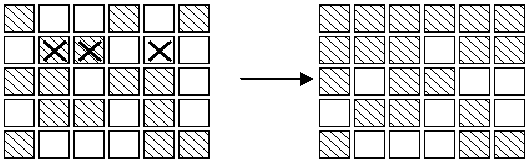
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged. 

Note: 
1. It does not matter what order the buttons are pressed. 
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once. 
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first 
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off. 
Write a program to solve the puzzle.

Input

The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.

Output

For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.

Sample Input

2
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
0 0 1 0 1 0
1 0 1 0 1 1
0 0 1 0 1 1
1 0 1 1 0 0
0 1 0 1 0 0

Sample Output

PUZZLE #1
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
PUZZLE #2
1 0 0 1 1 1
1 1 0 0 0 0
0 0 0 1 0 0
1 1 0 1 0 1
1 0 1 1 0 1

题意：一个5*6的矩阵，其中1代表灯亮，0代表灯灭，对于每一个开关布局，若b[i][j]==1，则a[i][j]与其相邻四个元素的值变化（0变1,1变0），现让你求出一个开关布局，使得每一个灯最后都是灭的。

记得以前写高代课作业的时候曾经写过一个消元法求答案的程序，没用结构体，一遇到分数就gg……这个题目作为消元法的入门题感觉着实有点难啊，它的运算不是加减乘除，是异或（虽然加法取摸也行）…没想到acm中将消元法的运算扩展了，更容易编码，但是构建方程组还是有点难想的……

这个题目有30个未知量，倒着想，最后状态全是0，对于答案矩阵c,0 xor c[i][j]  xor c[i-1][j] xor c[i+1][j] xor c[i][j-1] xor c[i][j+1] ==a[i][j]，其中a[i][j]为题目给出的输入。所以，每个方程中，只有5项的系数为1，其余全为零。设b为增广矩阵，a[i][j]的系数离散化到矩阵中的第6*i-6+j行，将a[i][j]放到b[6*i-6+j][31]中，这样就能构建出增广矩阵了。系数矩阵是不变的，如下：

至于消元法，高等代数中解释的很详细了，虽然不知道线性代数中是怎么讲的，但是

肯定也是讲过方法的，这里就不赘述了。

代码：

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
int a[35],x[40],map[10][10],b[35][35];  //b:系数矩阵的增广矩阵
    int i,j,k,m,n,t;

void gauss()
{
 int i,j,k;
 for(k=1;k<=30;k++)
   {for(i=k;i<=30;i++)
      if(b[i][k]==1)break;
    if(i!=k)
      for(j=1;j<=31;j++)swap(b[i][j],b[k][j]);
    for(i=1;i<=30;i++)
     if(i!=k && b[i][k]==1)
      for(j=1;j<=31;j++)b[i][j]=b[i][j]^b[k][j];    
   }
}


int main(int argc, char const *argv[])
{   
	
    scanf("%d",&t);
    for(int t1=1;t1<=t;t1++)
    { memset(a,0,sizeof(a));
      memset(x,0,sizeof(x));
      memset(b,0,sizeof(b));
      for(i=1;i<=5;i++)       //构建30*31的矩阵
      	for(j=1;j<=6;j++)
      		{scanf("%d",&map[i][j]);
      		 b[6*i-6+j][31]=map[i][j];
             b[6*i-6+j][6*i-6+j]=1;
             if(i>1)b[6*i-6+j][6*i-12+j]=1;
             if(i<=4)b[6*i-6+j][6*i+j]=1;
             if(j>1)b[6*i-6+j][6*i-6+j-1]=1;
             if(j<=5)b[6*i-6+j][6*i-6+j+1]=1; 
              }
      printf("PUZZLE #%d\n",t1);        
      gauss();
      for(i=1;i<=30;i++)
       if(i%6==0)printf("%d\n",b[i][31]);
        else printf("%d ",b[i][31]); 
     

    }
 	return 0;
}