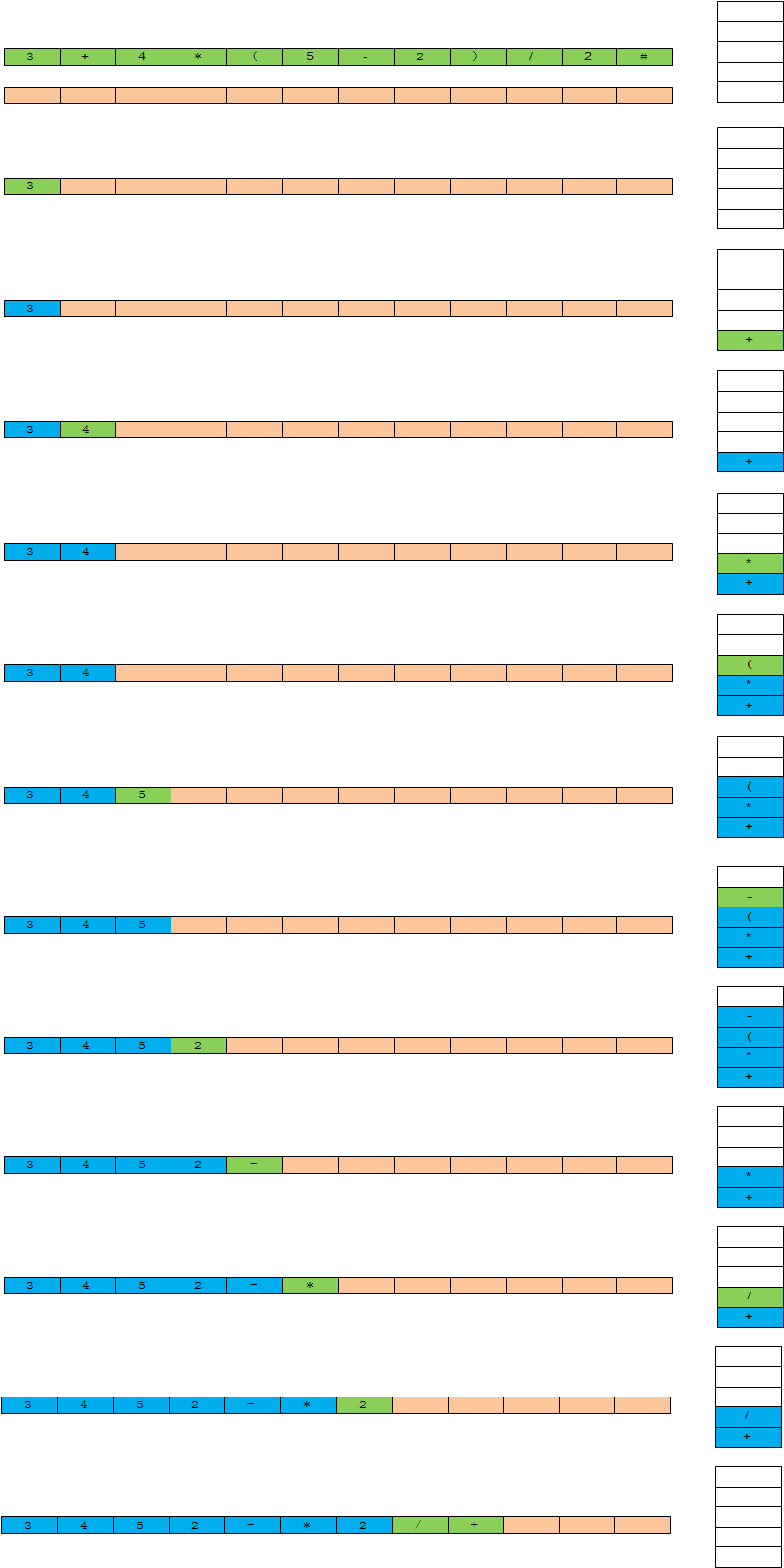逆波兰表示法
前言:
在逆波兰记法中,操作符置于操作数的后面。例如表达“三加四”时,写作“3 4 +”,而不是“3 + 4”。如果有多个操作符,操作符置于第二个操作数的后面,所以常规中缀记法的“3 - 4 + 5”在逆波兰记法中写作“3 4 - 5 +”:先3减去4,再加上5。使用逆波兰记法的一个好处是不需要使用括号。例如中缀记法中“3 - 4 * 5”与“(3 - 4)*5”不相同,但后缀记法中前者写做“3 4 5 * -”,无歧义地表示“3 (4 5 *) −”;后者写做“3 4 - 5 *”。
逆波兰表达式的解释器一般是基于堆栈的。解释过程一般是:操作数入栈;遇到操作符时,操作数出栈,求值,将结果入栈;当一遍后,栈顶就是表达式的值。因此逆波兰表达式的求值使用堆栈结构很容易实现,和能很快求值。
伪代码
- while有输入符号
- 读入下一个符号
- IF是一个操作数
- 入栈
- ELSE IF是一个操作符
- 有一个先验的表格给出该操作符需要n个参数
- IF堆栈中少于n个操作数
- (错误) 用户没有输入足够的操作数
- Else,n个操作数出栈
- 计算操作符。
- 将计算所得的值入栈
- IF栈内只有一个值
- 这个值就是整个计算式的结果
- ELSE多于一个值
- (错误) 用户输入了多余的操作数
例子
中缀表达式“5 + ((1 + 2) * 4) − 3”写作
- 5 1 2 + 4 * + 3 −
下表给出了该逆波兰表达式从左至右求值的过程,堆栈栏给出了中间值,用于跟踪算法。
| 输入 | 操作 | 堆栈 | 注释 |
|---|---|---|---|
| 5 | 入栈 | 5 | |
| 1 | 入栈 | 5, 1 | |
| 2 | 入栈 | 5, 1, 2 | |
| + | 加法运算 | 5, 3 | (1, 2)出栈;将结果(3)入栈 |
| 4 | 入栈 | 5, 3, 4 | |
| * | 乘法运算 | 5, 12 | (3, 4)出栈;将结果(12)入栈 |
| + | 加法运算 | 17 | (5, 12)出栈;将结果 (17)入栈 |
| 3 | 入栈 | 17, 3 | |
| − | 减法运算 | 14 | (17, 3)出栈;将结果(14)入栈 |
计算完成时,栈内只有一个操作数,这就是表达式的结果:14
public class Solution {
public static void main(String[] args){
String[] RPN = "5 1 -".split(" ");
System.out.println(new Test().calculateRPN(RPN));
}
public double calculateRPN(String[] RPN) {
assert (RPN != null && RPN.length != 0);
Stack<Double> stack = new Stack<Double>();
for (int i = 0; i < RPN.length; i++) {
if (isNumber(RPN[i])) {
stack.push(Double.parseDouble(RPN[i]));
} else {
double v1 = stack.pop();
double v2 = stack.pop();
double result = eval(RPN[i], v2, v1);
stack.push(result);
}
}
return stack.pop();
}
public boolean isNumber(String s) {
if (s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")) return false;
return true;
}
public static double eval(String op, double val1, double val2) {
if (op.equals("+")) return val1 + val2;
if (op.equals("-")) return val1 - val2;
if (op.equals("/")) return val1 / val2;
if (op.equals("*")) return val1 * val2;
throw new RuntimeException("Invalid operator");
}
}
逆波兰式的实现
在逆波兰式的实现中,最大的问题是如何改变运算符的先后顺序,把高优先级的运算符放在低优先级运算符的左侧。比如,有一个中缀表达式2 + 3 × 4,它所对应的逆波兰式应当是2 3 4 × +。在我们做中缀表达式到逆波兰式转换的时候,必须在不改变操作数顺序的情况下,把高优先级的乘法操作符移动到低优先级的加法运算符的左侧。
很自然的,我们会想到堆栈。堆栈具有后进先出的特点。所以我们可以设计一个符号栈,用于临时存储一个中缀表达式中的全部运算符;设计一个RPN数组,用于存储逆波兰式输出。然后从左向右扫描一个中缀表达式,并循环执行以下步骤:
1. 如果扫描到一个运算数,则将其放到RPN数组的末尾
2. 如果扫描到一个运算符。首先比较该运算符和符号栈栈顶运算符的优先级。如果符号栈栈顶运算符的优先级比较低,则将新运算符压入符号栈(这样最后将符号出栈时,高优先级符号先出栈)。如果栈顶符号的优先级更高,就把栈顶符号弹出,并放入RPN数组末尾。然后继续比较新扫描到的运算符和栈顶运算符的优先级,直到找到一个优先级比自己低的栈顶元素或者到达堆栈栈底。
3. 如果表达式扫描结束。将栈中操作符顺序弹出放到RPN数组中。这样就得到了一个逆波兰表达式。
如下是一个逆波兰式生成过程的实例。其中绿色部分代表每一步中发生变化的部分。其中特殊之处在于对括弧的处理,括弧的优先级高于所有操作符,但是括弧中所有的操作符优先级又高于括弧。所以当栈顶为括弧的时候,不会将括弧弹出,而是继续压栈。当弹出括弧的时候,也不会把括弧放入逆波兰式中。
原中缀表达式:3 + 4 × (5 - 2)/ 2
逆波兰表达式:3 4 5 2 - × 2 / +
public class Test {
public List<String> toPostfix(String[] in, HashMap<String, Integer> precedence) {
List<String> RPN = new ArrayList<String>();
Stack<String> ops = new Stack<String>();
for (int i = 0; i < in.length; i++) {
String s = in[i];
if (!precedence.containsKey(in[i])) {
RPN.add(s);
continue;
}
while(true) {
if (ops.isEmpty() || s.equals("(") || (precedence.get(s) > precedence.get(ops.peek()))) {
ops.push(s);
break;
}
String op = ops.pop();
if (op.equals("(")) {
break;
} else {
RPN.add(op);
}
}
}
while (!ops.isEmpty()) {
RPN.add(ops.pop());
}
return RPN;
}
public HashMap<String, Integer> priorityInfo(){
// precedence order of operators
HashMap<String, Integer> precedence = new HashMap<String, Integer>();
precedence.put("(", 0); // for convenience with algorithm
precedence.put(")", 0);
precedence.put("+", 1); // + and - have lower precedence than * and /
precedence.put("-", 1);
precedence.put("*", 2);
precedence.put("/", 2);
return precedence;
}
}
本文文字解释和图片来自WIKI和http://blog.csdn.net/jiangwlee/article/details/7182537