【LeetCode】Perfect Squares 解题报告
Perfect Squares
[LeetCode]
https://leetcode.com/problems/perfect-squares/
Total Accepted: 15606 Total Submissions: 53625 Difficulty: Medium
Question
Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, …) which sum to n.
Examples
For example, given
n = 12, return3because12 = 4 + 4 + 4; givenn = 13, return2because13 = 4 + 9.
Ways
方法一
动态规划。
如果一个数x可以表示为一个任意数a加上一个平方数bxb,也就是x=a+bxb,那么能组成这个数x最少的平方数个数,就是能组成a最少的平方数个数加上1(因为b*b已经是平方数了)。
public static int numSquares(int n) {
int[] dp = new int[n + 1];
// 将所有非平方数的结果置最大,保证之后比较的时候不被选中
Arrays.fill(dp, Integer.MAX_VALUE);
// 将所有平方数的结果置1
for (int i = 0; i * i <= n; i++) {
dp[i * i] = 1;
}
// 从小到大找任意数a
for (int a = 0; a <= n; a++) {
// 从小到大找平方数bxb
for (int b = 0; a + b * b <= n; b++) {
// 因为a+b*b可能本身就是平方数,所以我们要取两个中较小的
dp[a + b * b] = Math.min(dp[a] + 1, dp[a + b * b]);
System.out.println(a + b * b + ":--" + Arrays.toString(dp));
}
}
return dp[n];
}
看下输出就明白了:
0:--[1, 1, 2147483647, 2147483647, 1, 2147483647, 2147483647, 2147483647, 2147483647, 1, 2147483647]
1:--[1, 1, 2147483647, 2147483647, 1, 2147483647, 2147483647, 2147483647, 2147483647, 1, 2147483647]
4:--[1, 1, 2147483647, 2147483647, 1, 2147483647, 2147483647, 2147483647, 2147483647, 1, 2147483647]
9:--[1, 1, 2147483647, 2147483647, 1, 2147483647, 2147483647, 2147483647, 2147483647, 1, 2147483647]
1:--[1, 1, 2147483647, 2147483647, 1, 2147483647, 2147483647, 2147483647, 2147483647, 1, 2147483647]
2:--[1, 1, 2, 2147483647, 1, 2147483647, 2147483647, 2147483647, 2147483647, 1, 2147483647]
5:--[1, 1, 2, 2147483647, 1, 2, 2147483647, 2147483647, 2147483647, 1, 2147483647]
10:--[1, 1, 2, 2147483647, 1, 2, 2147483647, 2147483647, 2147483647, 1, 2]
2:--[1, 1, 2, 2147483647, 1, 2, 2147483647, 2147483647, 2147483647, 1, 2]
3:--[1, 1, 2, 3, 1, 2, 2147483647, 2147483647, 2147483647, 1, 2]
6:--[1, 1, 2, 3, 1, 2, 3, 2147483647, 2147483647, 1, 2]
3:--[1, 1, 2, 3, 1, 2, 3, 2147483647, 2147483647, 1, 2]
4:--[1, 1, 2, 3, 1, 2, 3, 2147483647, 2147483647, 1, 2]
7:--[1, 1, 2, 3, 1, 2, 3, 4, 2147483647, 1, 2]
4:--[1, 1, 2, 3, 1, 2, 3, 4, 2147483647, 1, 2]
5:--[1, 1, 2, 3, 1, 2, 3, 4, 2147483647, 1, 2]
8:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
5:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
6:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
9:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
6:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
7:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
10:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
7:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
8:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
8:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
9:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
9:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
10:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
10:--[1, 1, 2, 3, 1, 2, 3, 4, 2, 1, 2]
2
但是此方法时间复杂度O(n^2).提交时时间溢出。
方法二
这道题是考察四平方和定理,说明每个正整数均可表示为4个整数的平方和。
根据四平方和定理,任意一个正整数均可表示为4个整数的平方和,其实是可以表示为4个以内的平方数之和,那么就是说返回结果只有1,2,3或4其中的一个,首先我们将数字化简一下,由于一个数如果含有因子4,那么我们可以把4都去掉,并不影响结果,比如2和8,3和12等等,返回的结果都相同,读者可自行举更多的栗子。还有一个可以化简的地方就是,如果一个数除以8余7的话,那么肯定是由4个完全平方数组成,这里就不证明了,因为我也不会证明,读者可自行举例验证。那么做完两步后,一个很大的数有可能就会变得很小了,大大减少了运算时间,下面我们就来尝试的将其拆为两个平方数之和,如果拆成功了那么就会返回1或2,因为其中一个平方数可能为0.
public class Solution {
public int numSquares(int n) {
while (n % 4 == 0) n /= 4;
if (n % 8 == 7) return 4;
for (int a = 0; a * a < n; a++) {
for (int b = 0; b * b <= n - a * a; b++) {
if (a * a + b * b == n) {
return (a > 0 ? 1 : 0) + (b > 0 ? 1 : 0);
}
}
}
return 3;
}
}
这个方法3ms。
Solution
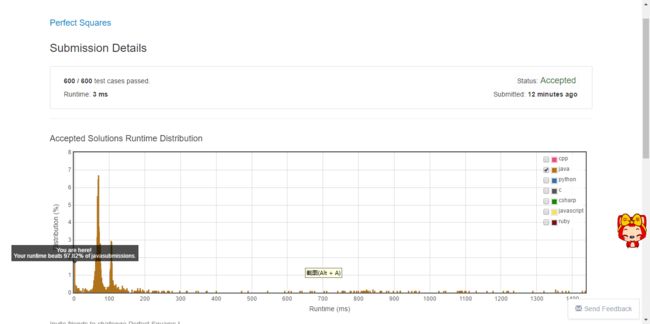
动态规划的方法很慢,方法二这个投机取巧的方法得到了3ms,超过97%用户。
分享一下刚开始的初步的没有优化过的方法二,下面代码效率较慢(21ms)。好的方法请看上面的代码。说明代码优化很重要。
public class Solution {
public int numSquares(int n) {
while (n % 4 == 0) n /= 4;
if (n % 8 == 7) return 4;
for (int a = 0; a * a <= n; a++) {
for (int b = 0; b <= n; b++) {
if (a * a + b * b == n) {
return (a > 0 ? 1 : 0) + (b > 0 ? 1 : 0);
}
}
}
return 3;
}
}
Captures
测试结果截图:
Reference
http://segmentfault.com/a/1190000003768736#articleHeader1
http://www.cnblogs.com/grandyang/p/4800552.html
Date
2015/11/15 20:43:42
2016/4/29 21:05:01