高精度标定和效验三维相位轮廓测量系统
高精度标定和效验三维相位轮廓测量系统
为了提高三维相位轮廓测量系统的测量精度,提出了一种系统标定的理论模型,并且实验验证了其正确性。为了进一步验证系统精度,使用空间上随机放置的1个和2个轴承滚珠,通过对滚珠的测量和分析,验证了标定方法的有效性。这种三维相位轮廓测量系统的标定和效验方法为它的应用提供了新的技术方案。
关键词:三维相位轮廓测量法,标定,精度效验
Abstract
In order to improve the accuracy of the 3D phase profilometry system,a theoretical model for the system calibration ispresented.Experiments are done for the verification of its correctness.Furthermore,to validate system accuracy,randomlyplaced ball bearings are used to verify the validity of the calibration method。through the measurement and analysis.The 3Dphase profitometry system calibration and efficacy methods in this paper provide a new technical so!ution for its application.
Keywords:phase profilometry measurement。calibration.verification the accuracy
二十世纪八十年代初,V.Srinivasna和M.Haliuoas等人将激光相移干涉算法和原理引入对物体表面三维轮廓测量中[t--3],称为相位轮廓测量法(PMP:Phase Measurement Profilome—try)。它的最大优点在于求解物体初相位时是点对点的运算,即任一点的相位值不受相邻点光强值的影响,从而避免了物面反射率不均匀引起的误差。相位轮廓测量法一次就可测量出物体的整个表面,具有速度快、精度高和抗干扰能力强的优点,已经得到了广泛的应用。今后的一个重要发展方向是改进标定方法,提高测量精度[2】。大小的球作为标定物,将圆的霍夫变换拓展到三维空间,并用于对球体半径的识别,提出了一套相位轮廓测量快速标定方法M],特点是标定系统简单,自己形成参考坐标系。Z.Wang等提出了一种快速精确测量的新方法(5】,系统中的投影仪和摄像机可以随意放置,他们采用多频投影条纹以及逆向自标定方法,在实验中测量速度可大于每秒两幅三维图像。四川大学的X.Su教授小组在相位轮廓测量法方面也做了很多出色的工作,他们提出了一种影射算法用于相位测量轮廓嘲,其利用了相位一高度的影射关系,通过测量几个不同平行平面的相位来获得相位一高度的影射公式,而不是测量系统的几何参数,从而减少了标定所需时间,同时减小了误差。W.Su等提出了一种应用于测量不连续高度、阶梯形物体的相位轮廓测量系统的标定方法【7]。本文基于X.Su提出的隐式相位一高度的影射关系,借助于精确的相位展开方法,对系统进行了标定,并对摄像机坐标系和实际坐标系坐标轴之间出现的夹角进行了修正,从而提高了测量精度。实验测量了不同位置球体的三维坐标,通过对球体半径的分析,从而效验三维相位轮廓测量系统的精度。
1 三维相位轮廓测量系统构成
三维相位轮廓测量系统结构如图1a所示,投影和摄像机安装在铝合金多维度调整桁架上,可以分别对投影仪和摄像机的高度和两维仰角实现三自由度高精度调整,并且可以独立调整它们之间的距离。摄像机是MegaPlus ES 1.0,空间分辨率1008(H) ×1018(V),动态范围>58dB。摄像机与计算机的连接使用加拿大Matrox Graphics Inc.的Meteor II Digital 4L图像采集卡。正弦条纹投影使用Plus V1 100数字投影仪,亮度1000流明,对比度为2000:1。标定单元使用一个两维(X,y)手动平台,精度±O.01mm,行程0-180mm。平台上有一固定平板,平板垂直于摄像机光轴放置,如图1b中自板。
2 三维相位轮廓测量法原理
如图1所示,当正弦光栅条纹投影到三维漫反射物体表面时,所探测的正弦光栅受物体表面高度调制,在CCD相机像平面上成像。在实际应用中,投影仪投影j-1,⋯,N个条纹图像,可以用下式表示:
![]()
式中A(x,Y)为背景光强,B(X,y)为条纹的调制深度,相位函数4Kx,y)是由物体三维面形z=h(X,y)所决定的条纹相位变形,8{是每次投影的附加相移。巾(x,Y)与三维面形之间的关系取决与系统的结构参数。为了正确解调出相位函数由(x,Y),要求探测的光强应与巾(x,Y)的关系严格满足(1)式,尽可能避免l(X,y)的高次谐波而引人相位误差[3】。相移理论如下:
3 三维相位轮廓测量系统的标定
3.1标定Z坐标
相位轮廓测量系统采用共面光轴模型,通过此模型得到了一个有效隐式相位一高度映射关系:
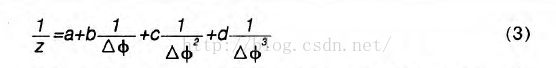
其中a、b、c、d是与整个系统有关的三个待定参数。△书是各平面相对于参考平面的相位值,分别对应标定时3个不同Z位置的相位值,这样形成3元方程组,可以求解出系统参数a,b,c,d。那么高度Z与像素平面各点的关系z(m,n)就已知了,只需再知道各个像素点与坐标X,Y的关系,那么每个像素点对应的空间坐标也就确定了,从而整个系统的标定工作也就完成了。
为了获得Z与像素坐标的关系,将标定平板放在Z轴上6个不同位置(0mm、20mm、40mm、60mm、80mm、100mm),分别测量z位置处标定平面的空间相位值。求解(2)式方程组中的系数a,b,c,d。为了检验标定的精度,我们将标定平面固定在位置z=68.9mm处,测量其空间相位值,然后根据标定式(2)求得标定平面上各点的Z坐标及的实体偏差,实验结果如图2所示,Z坐标的测量精度达到了10-2mm级。
3.2标定X,Y坐标
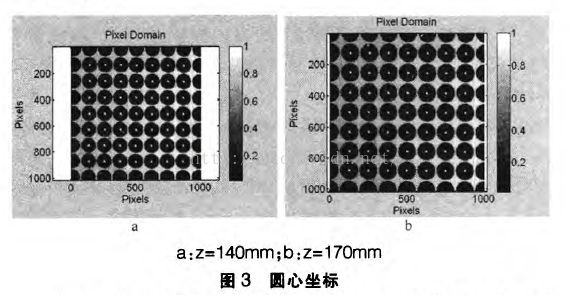
在标定平面上等间距的画一些圆,平板上所有的圆心坐标和半径都是已知的,如图1c所示。然后标定平板沿Z方向在导轨上移动,采集对应的多组圆心坐标的数据m;,n;,X;,Yt(i=1,2,⋯,k)。x,Y空间坐标与m,n像素坐标的关系为:

利用测得的多组数据,进行最4xZ.乘法拟合,如图3所示。最终拟合得到其中的系数ao、a,、a2和b。、b,、b2,完成了对系统的标定工作。
对于每个圆心的像素坐标以及其相应的Z轴坐标,其可拟和成一条直线。通过直线拟合,分别得到了空间坐标X、Y与像素坐标m、n的关系:

对于拟和方程x=ao+alm+a2n而言,每个像素坐标(m,n)的X值与拟和值的偏离值为:
则X的剩余标准偏差,或简称标准偏差:

x=ao+a,m+a2n的标准偏差为:Sx=+O.024mm。同理,对于拟和方程y=bo+blm+b2n而言,它的标准偏差为:Sv=±0.022mm。
3.3修正倾角
标定之前我们假设了摄像机坐标系和实际空间坐标系的坐标轴平行,但是由于导轨一靶标系统和摄像机一投影仪系统并不固定在一起,实验中两系统的摆放不可避免的使两坐标系的z轴总会出现夹角,我们将对其进行修正。由前可知,摄像机的光轴方向以及物体的高度方向即分别为摄像机坐标系和实际坐标系的Z轴。假定两坐标轴平行,拍摄两幅不同的Z位置的标定平板,通过拟合出圆心坐标,则有两幅图的中心坐标重合为一点。根据此原理,拍摄z=140mm以及z=170mm处的标定平板,拟合球心坐标,分别得到图3所示。由于本实验所采用的摄像机的视场大小1008$1018像素,则摄像机理论中心坐标为(504,509)。通过MTALAB编写程序拟合两幅图的圆心坐标,并拟合出实际坐标,通过与理论值对比确定系统的精确性。拟合两幅图圆心坐标,得到圆心位移和圆心位移误差如图4所示。
此时,X方向的偏角ox,Y方向的偏角0。分别为:

其中d=lOOmm,0。=0.019rad,0。=0.009rad。倾角的标准方差分别为:x方向:±7.902xlO-4rad;y方向:±4.323x10-4rad。在算出的坐标后,乘以倾角转动矩阵对坐标做出修正。
4 实验结果及误差分析
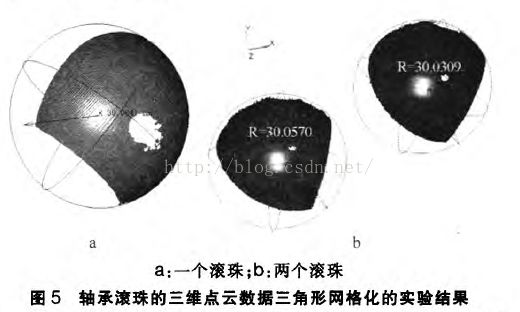
为了检验整个系统的测量精度,我们使用直径为30±0.01 mm的轴承滚珠做效验标准件,特点是它们的半径不受它们所处位置影响。图5a是实验测量的一个轴承滚珠部分球冠由三维点云数据三角形网格化后的三维矢量图形,中间数据缺失部分是球体反光所致。通过拟合得到球体的半径是30.084mm。
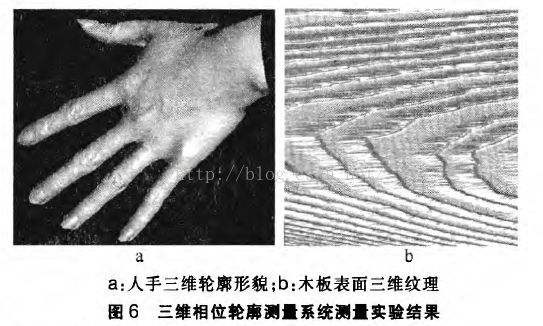
图5b是将2个轴承滚珠在高低和左右两个方向随机错开放置,测得和拟合出的球体半径分别是30.057mm和30 031mm。测量结果在误差范围内,系统精度达到设计要求。图6a是使用上述标定后的相位轮廓测量系统,测量人手的三维轮廓形貌,人手的皱褶清晰可见;图6b测量普通木板的三维纹理。由于整个视场为250mmx240mm,所以证明该系统的测量精度和分辨率较高。
5结束语
本文提出使用轴承滚珠检验系统的测量精度,并分别测量了1个和2个半径为30mm的轴承滚珠,轴承滚珠半径测量误
差为10_2mm级别,证明的三维相位轮廓测量系统和标定方法达到了较高测量精度。从而为使三维相位轮廓测量方法进一步应用到高精度测量领域提供了技术支持。
参考文献
略。。。
------------------------------------------------------------
该传递函数存在两个位于虚轴上的极点,用其设计出来的线性控制器应用到非线性系统中鲁棒性不够强。为设计出鲁棒性较强的控制器,将该传递函数中的一个极点向左半平面移动,应用Bode图近似方法,将传递函数变换为:

取悬浮控制器的有效带宽频率为100rad/s,则T1=O.01,结合式(5)和(6),得到一个PD控制器:

其中8,是设定气隙值。将线性控制律v=K(8r-8)代入式(2),得到非线性控制律:
4仿真分析
fd=O.5mg时的仿真情况如图2所示,fg=mg时的仿真情况如图3所示。
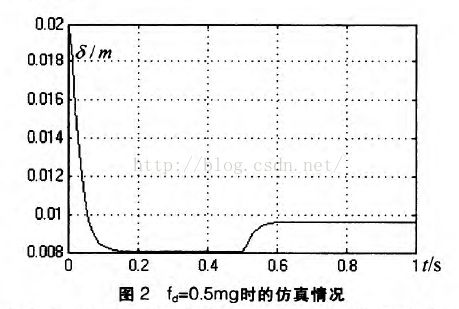
仿真时间共1S,其中在0.5s以前,采用根据线性模型设计出的控制器对非线性模型进行控制,这相当于对具有摄动的模型进行控制,得到的气隙输出与设定值的误差为0,无超调,上升时间≤O.1s;
在0.5s时在非线性模型上增加了恒值干扰,气隙输出偏离设定值,但是比较稳定。这些仿真结果说明该控制器具有良好的鲁棒性。
参考文献
略。。。