图像相似度计算

本文转自http://blog.sina.com.cn/s/blog_4a540be60100vjae.html

图像相似度计算主要用于对于两幅图像之间内容的相似程度进行打分，根据分数的高低来判断图像内容的相近程度。

 

   可以用于计算机视觉中的检测跟踪中目标位置的获取，根据已有模板在图像中找到一个与之最接近的区域。然后一直跟着。已有的一些算法比如BlobTracking，Meanshift，Camshift，粒子滤波等等也都是需要这方面的理论去支撑。

 

  还有一方面就是基于图像内容的图像检索，也就是通常说的以图检图。比如给你某一个人在海量的图像数据库中罗列出与之最匹配的一些图像，当然这项技术可能也会这样做，将图像抽象为几个特征值，比如Trace变换，图像哈希或者Sift特征向量等等，来根据数据库中存得这些特征匹配再返回相应的图像来提高效率。

 

  下面就一些自己看到过的算法进行一些算法原理和效果上的介绍。

 

   (1)直方图匹配。

 

      比如有图像A和图像B，分别计算两幅图像的直方图，HistA，HistB，然后计算两个直方图的归一化相关系数（巴氏距离，直方图相交距离）等等。

 

      这种思想是基于简单的数学上的向量之间的差异来进行图像相似程度的度量，这种方法是目前用的比较多的一种方法，第一，直方图能够很好的归一化，比如通常的256个bin条的。那么两幅分辨率不同的图像可以直接通过计算直方图来计算相似度很方便。而且计算量比较小。

 

      这种方法的缺点:

 

         1、直方图反映的是图像像素灰度值的概率分布，比如灰度值为200的像素有多少个，但是对于这些像素原来的位置在直方图中并没有体现，所以图像的骨架，也就是图像内部到底存在什么样的物体，形状是什么，每一块的灰度分布式什么样的这些在直方图信息中是被省略掉得。那么造成的一个问题就是，比如一个上黑下白的图像和上白下黑的图像其直方图分布是一模一样的，其相似度为100%。

 

         2、两幅图像之间的距离度量，采用的是巴氏距离或者归一化相关系数，这种用分析数学向量的方法去分析图像本身就是一个很不好的办法。

 

         3、就信息量的道理来说，采用一个数值来判断两幅图像的相似程度本身就是一个信息压缩的过程，那么两个256个元素的向量（假定直方图有256个bin条）的距离用一个数值表示那么肯定就会存在不准确性。

 

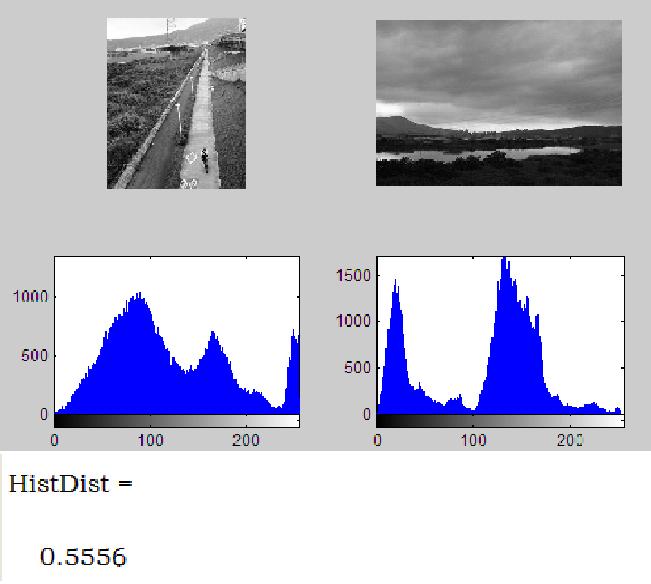
   下面是一个基于直方图距离的图像相似度计算的Matlab Demo和实验结果.

%计算图像直方图距离
%巴氏系数计算法

M=imread('1.jpg');
N=imread('2.jpg');
I=rgb2gray(M);
J=rgb2gray(N);

[Count1,x]=imhist(I);
[Count2,x]=imhist(J);
Sum1=sum(Count1);Sum2=sum(Count2);
Sumup = sqrt(Count1.*Count2);
SumDown = sqrt(Sum1*Sum2);
Sumup = sum(Sumup);
figure(1);
subplot(2,2,1);imshow(I);
subplot(2,2,2);imshow(J);
subplot(2,2,3);imhist(I);
subplot(2,2,4);imhist(J);
HistDist=1-sqrt(1-Sumup/SumDown)

 

 

  

 

   通过上图可以看到这种计算图像相似度的方法确实存在很大的弊端。然而很多人也对于这种方法进行了修改，比如FragTrack算法，具体可以参见这篇论文《》。其中对图像分成横纵的小块，然后对于每一个分块搜索与之最匹配的直方图。来计算两幅图像的相似度，融入了直方图对应位置的信息。但是计算效率上很慢。

  还有一种是计算一个图像外包多边形，一般得到跟踪图像的前景图后计算其外包多边形，根据外包多边形做Delauny三角形分解，然后计算每个三角形内部的直方图，对于这两个直方图组进行相似距离计算。这样就融入了直方图的位置信息。

 (2)数学上的矩阵分解

   图像本身就是一个矩阵，可以依靠数学上矩阵分解的一些知识来获取矩阵中一些代表这个矩阵元素值和分布的一些鲁棒性特征来对图像的相似度进行计算。

    最常用的一般是SVD分解和NMF分解。

   下面简单介绍下SVD分解的一些性质，如果需要探究的更深入一点网上有一些相关文献，读者可以去探究的更清楚：

 <1> 奇异值的稳定性

 <2> 奇异值的比例不变性

 <3> 奇异值的旋转不变性

 <4> 奇异值的压缩性        

    综上所述，可以看出奇异值分解是基于整体的表示。图像奇异值特征向量不但具有正交变换、旋转、位移、镜像映射等代数和几何上的不变性,而且具有良好的稳定性和抗噪性，广泛应用于模式识别与图像分析中。对图像进行奇异值分解的目的是：得到唯一、稳定的特征描述；降低特征空间的维数；提高抵抗干扰和噪声的能力。但是由于奇异值分解得到的奇异矢量中有负数存在所以不能很好的解释其物理意义。

  非负矩阵分解(NMF):

    NMF的主要思想是将非负矩阵分解为可以体现图像主要信息的基矩阵与系数矩阵，并且可以对基矩阵赋予很好的解释，比如对人脸的分割，得到的基向量正是人的“眼睛”，“鼻子”等主要概念特征，源图像表示为这些特征的加权组合。所以NMF算法也在人脸识别等场合中发挥着巨大的作用。

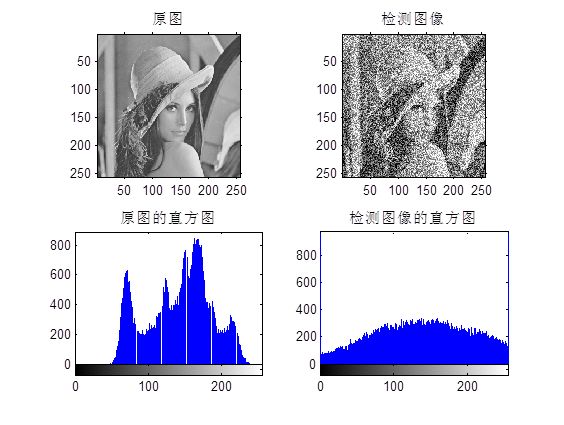
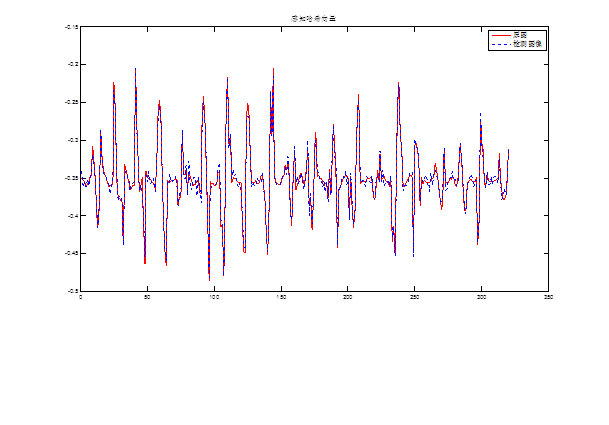
   下面一个实验说明了SVD+NMF数学上的这些分解在图像相似度判定方面的应用，这个跟我目前的课题有关细节方面就不再透露更多了。

当然基于数学上的矩阵特征值计算的还有很多方法比如Trace变换，不变矩计算等等，当然如果有需要这方面资料的同学可以找我，我可以进行相关的帮助。

（3）基于特征点的图像相似度计算

    每一幅图像都有自己的特征点，这些特征点表征图像中比较重要的一些位置，比较类似函数的拐点那种，通常比较常用的有Harris角点和Sift特征点。那么将得到的图像角点进行比较，如果相似的角点数目较多，那么可以认为这两幅图像的相似程度较高。这里主要介绍基于Sift算子。

   对于Sift的原理和代码可以参见David Lower的网站。

David G Lowe Sift网站

   那么我们就可以通过找到匹配点的个数来判断两幅图像是否一致，这个算法的好处是对于一个物体，两个不同角度下得到的照片依然可以找到很多的匹配点，我也一直认为是一个综合来说结果相对较为准确的方法，但是由于每个特征点需要计算一个长度不小的特征值，也造成了该算法的时间消耗比较大。所以不常用于实时的视频处理。这个算法还有一个好处就是可以通过找到的匹配特征点进行图像校正。关于使用Sift做图像校正请参见我的另外一篇博文。

  

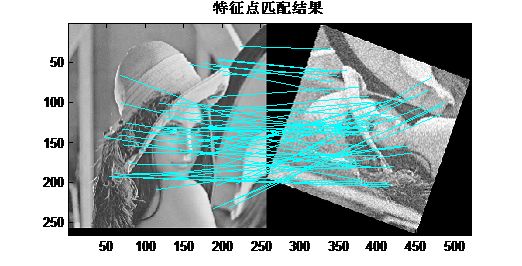
我当时对于比如左边图像，找到50个特征点，如果其中有60%以上的与右边的匹配上了，认为两幅图像是相似图像。

上图使用Sift找到的匹配对应点，然后通过仿射变换的6维参数计算，然后逆变换得到校正后的图像，效果蛮不错的，可见Sift对于抗旋转和噪声的效果确实很好。

对于Sift也不能全部相信，一般使用RANSAC对于错误匹配点去除可以达到更好的效果，当然目前也有很多对SIFT进行改进的算法。希望有这方面研究的可以多多交流。