集训队专题（5.1）1008 Graph Coloring

Graph Coloring

Time Limit : 2000/1000ms (Java/Other)   Memory Limit : 20000/10000K (Java/Other)

Total Submission(s) : 35   Accepted Submission(s) : 14

Special Judge

Problem Description

You are to write a program that tries to find an optimal coloring for a given graph. Colors are applied to the nodes of the graph and the only available colors are black and white. The coloring of the graph is called optimal if a maximum of nodes is black. The coloring is restricted by the rule that no two connected nodes may be black. 


 
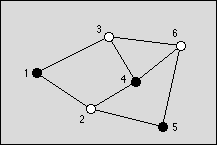
Figure 1: An optimal graph with three black nodes 

 

Input

The graph is given as a set of nodes denoted by numbers 1...n, n <= 100, and a set of undirected edges denoted by pairs of node numbers (n1, n2), n1 != n2. The input file contains m graphs. The number m is given on the first line. The first line of each graph contains n and k, the number of nodes and the number of edges, respectively. The following k lines contain the edges given by a pair of node numbers, which are separated by a space.

 

Output

The output should consists of 2m lines, two lines for each graph found in the input file. The first line of should contain the maximum number of nodes that can be colored black in the graph. The second line should contain one possible optimal coloring. It is given by the list of black nodes, separated by a blank.

 

Sample Input

   
   
   
   

    
    
    
    1
6 8
1 2
1 3
2 4
2 5
3 4
3 6
4 6
5 6
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    3
1 4 5
   
   
   
   

 

Source

PKU

 

此题不难看出，题目要求我们求出最大独立集，这里我们需要借助一个定理，那就是：一个图的最大团就是其补图的最大独立集，而一个图的最大独立集就是其补图的最大团。这个定理应该很好理解，一个团的所有点都是两两连接的，若取其补图，肯定是两两都没有连接。所以此题我们只需要在输入的时候建立其补图，然后套小编的最大团模板就搞定了。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=106;
int g[maxn][maxn],dp[maxn],stk[maxn][maxn],mx;
int path[maxn],res[maxn];//记录最大团的点 
int dfs(int n,int ns,int dep)//
{
	if(ns == 0)
	{
		if(dep > mx)
		{
			swap(path,res);
			mx = dep;
			return 1;
		}
		return 0;
	}
	int i,j,k,p,cnt;
	for(i=0; i<ns; i++)
	{
		k = stk[dep][i];
		cnt = 0;
		if(dep + n - k <= mx) return 0;// 剪枝1， 若当前 顶点数量cnt 加上还能够增加的最大数量 仍小于 best则 退出并返回
		if(dep + dp[k] <= mx) return 0;// 剪枝2， 若当前 顶点数量cnt 加上 包含adj[i]的最大团顶点数 仍小于 best则 退出并返回
		for(j=i+1; j<ns; j++)
		{
			p = stk[dep][j];
			if(g[k][p]) stk[dep+1][cnt++] = p;
		}
		path[dep+1] = k;
		if( dfs(n,cnt,dep+1) ) return 1;
	}
	return 0;
}
int clique(int n)
{
	int i,j,ns;
	for(mx=0, i=n-1; i>=0; i--)
	{
		path[1] = i;
		for(ns=0, j=i+1; j<n; j++)// 遍历 [i+1, n] 间顶点
			if(g[i][j]) stk[1][ns++] = j;
		dfs(n,ns,1);
		dp[i] = mx;// 得出顶点 i, 出发构成最大团 中顶点数量
	}
	return mx;
}
int main()
{
	int n,T,m;
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&n,&m);
		memset(g,1,sizeof(g));
		for(int i=0; i<m; i++)
		{
			int x,y;
			scanf("%d%d",&x,&y);
			x--,y--;
			g[x][y] = g[y][x] = 0;
		}
		int ans = clique(n);
		printf("%d\n",ans);
		for(int i=1; i<=ans; i++)
		{
			printf("%d",res[i]+1);
			if(i == ans) printf("\n");
			else printf(" ");
		}
	}
	return 0;
}