Floyd-Warshall算法

loyd-Warshall算法，简称Floyd算法，用于求解任意两点间的最短距离，时间复杂度为O(n^3)。我们平时所见的Floyd算法的一般形式如下：

1 void  Floyd(){
2      int  i,j,k;
3      for (k = 1 ;k <= n;k ++ )
4          for (i = 1 ;i <= n;i ++ )
5              for (j = 1 ;j <= n;j ++ )
6                  if (dist[i][k] + dist[k][j] < dist[i][j])
7                      dist[i][j] = dist[i][k] + dist[k][j];
8  }

  注意下第6行这个地方，如果dist[i][k]或者dist[k][j]不存在，程序中用一个很大的数代替。最好写成if(dist[i][k]!=INF && dist[k][j]!=INF && dist[i][k]+dist[k][j]<dist[i][j])，从而防止溢出所造成的错误。
  上面这个形式的算法其实是Floyd算法的精简版，而真正的Floyd算法是一种基于DP(Dynamic Programming)的最短路径算法。
  设图G中n 个顶点的编号为1到n。令c [i, j, k]表示从i 到j 的最短路径的长度，其中k 表示该路径中的最大顶点，也就是说c[i,j,k]这条最短路径所通过的中间顶点最大不超过k。因此，如果G中包含边<i, j>，则c[i, j, 0] =边<i, j> 的长度；若i= j ，则c[i,j,0]=0；如果G中不包含边<i, j>，则c (i, j, 0)= +∞。c[i, j, n] 则是从i 到j 的最短路径的长度。
  对于任意的k>0，通过分析可以得到：中间顶点不超过k 的i 到j 的最短路径有两种可能：该路径含或不含中间顶点k。若不含，则该路径长度应为c[i, j, k-1]，否则长度为 c[i, k, k-1] +c [k, j, k-1]。c[i, j, k]可取两者中的最小值。
  状态转移方程：c[i, j, k]=min{c[i, j, k-1], c [i, k, k-1]+c [k, j, k-1]}，k＞0。
  这样，问题便具有了最优子结构性质，可以用动态规划方法来求解。

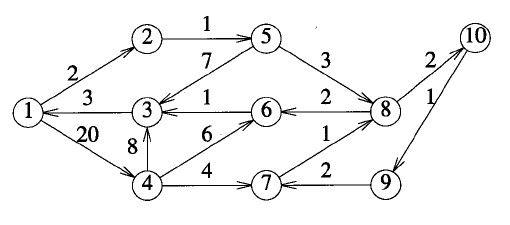
为了进一步理解，观察上面这个有向图：若k=0, 1, 2, 3，则c[1,3,k]= +∞；c[1,3,4]= 28；若k = 5, 6, 7，则c [1,3,k] = 10；若k=8, 9, 10，则c[1,3,k] = 9。因此1到3的最短路径长度为9。
  下面通过程序来分析这一DP过程，对应上面给出的有向图：

 

 

 1  #include  < iostream >
 2  using  namespace  std;
 3 
 4  const  int  INF  =   100000 ;
 5  int  n = 10 ,map[ 11 ][ 11 ],dist[ 11 ][ 11 ][ 11 ];
 6  void  init(){
 7      int  i,j;
 8      for (i = 1 ;i <= n;i ++ )
 9          for (j = 1 ;j <= n;j ++ )
10              map[i][j] = (i == j) ? 0 :INF;
11      map[ 1 ][ 2 ] = 2 ,map[ 1 ][ 4 ] = 20 ,map[ 2 ][ 5 ] = 1 ;
12      map[ 3 ][ 1 ] = 3 ,map[ 4 ][ 3 ] = 8 ,map[ 4 ][ 6 ] = 6 ;
13      map[ 4 ][ 7 ] = 4 ,map[ 5 ][ 3 ] = 7 ,map[ 5 ][ 8 ] = 3 ;
14      map[ 6 ][ 3 ] = 1 ,map[ 7 ][ 8 ] = 1 ,map[ 8 ][ 6 ] = 2 ;
15      map[ 8 ][ 10 ] = 2 ,map[ 9 ][ 7 ] = 2 ,map[ 10 ][ 9 ] = 1 ;
16  }
17  void  floyd_dp(){
18      int  i,j,k;
19      for (i = 1 ;i <= n;i ++ )
20          for (j = 1 ;j <= n;j ++ )
21              dist[i][j][ 0 ] = map[i][j];
22      for (k = 1 ;k <= n;k ++ )
23          for (i = 1 ;i <= n;i ++ )
24              for (j = 1 ;j <= n;j ++ ){
25                  dist[i][j][k] = dist[i][j][k - 1 ];
26                  if (dist[i][k][k - 1 ] + dist[k][j][k - 1 ] < dist[i][j][k])
27                      dist[i][j][k] = dist[i][k][k - 1 ] + dist[k][j][k - 1 ];
28              }
29  }
30  int  main(){
31      int  k,u,v;
32      init();
33      floyd_dp();
34      while (cin >> u >> v,u || v){
35          for (k = 0 ;k <= n;k ++ ){
36              if (dist[u][v][k] == INF) cout << " +∞ " << endl;
37              else  cout << dist[u][v][k] << endl;
38          }
39      }
40      return   0 ;
41  }

 

  输入 1 3
  输出 +∞
            +∞
            +∞
            +∞
            28
            10
            10
            10
            9
            9
            9

  Floyd-Warshall算法不仅能求出任意2点间的最短路径，还可以保存最短路径上经过的节点。下面用精简版的Floyd算法实现这一过程，程序中的图依然对应上面的有向图。

 

 1  #include  < iostream >
 2  using  namespace  std;
 3 
 4  const  int  INF  =   100000 ;
 5  int  n = 10 ,path[ 11 ][ 11 ],dist[ 11 ][ 11 ],map[ 11 ][ 11 ];
 6  void  init(){
 7      int  i,j;
 8      for (i = 1 ;i <= n;i ++ )
 9          for (j = 1 ;j <= n;j ++ )
10              map[i][j] = (i == j) ? 0 :INF;
11      map[ 1 ][ 2 ] = 2 ,map[ 1 ][ 4 ] = 20 ,map[ 2 ][ 5 ] = 1 ;
12      map[ 3 ][ 1 ] = 3 ,map[ 4 ][ 3 ] = 8 ,map[ 4 ][ 6 ] = 6 ;
13      map[ 4 ][ 7 ] = 4 ,map[ 5 ][ 3 ] = 7 ,map[ 5 ][ 8 ] = 3 ;
14      map[ 6 ][ 3 ] = 1 ,map[ 7 ][ 8 ] = 1 ,map[ 8 ][ 6 ] = 2 ;
15      map[ 8 ][ 10 ] = 2 ,map[ 9 ][ 7 ] = 2 ,map[ 10 ][ 9 ] = 1 ;
16  }
17  void  floyd(){
18      int  i,j,k;
19      for (i = 1 ;i <= n;i ++ )
20          for (j = 1 ;j <= n;j ++ )
21              dist[i][j] = map[i][j],path[i][j] = 0 ;
22      for (k = 1 ;k <= n;k ++ )
23          for (i = 1 ;i <= n;i ++ )
24              for (j = 1 ;j <= n;j ++ )
25                  if (dist[i][k] + dist[k][j] < dist[i][j])
26                      dist[i][j] = dist[i][k] + dist[k][j],path[i][j] = k;
27  }
28  void  output(int  i,int  j){
29      if (i == j) return ;
30      if (path[i][j] == 0 ) cout << j << '   ' ;
31      else {
32          output(i,path[i][j]);
33          output(path[i][j],j);
34      }
35  }
36  int  main(){
37      int  u,v;
38      init();
39      floyd();
40      while (cin >> u >> v,u || v){
41          if (dist[u][v] == INF) cout << " No path " << endl;
42          else {
43              cout << u << '   ' ;
44              output(u,v);
45              cout << endl;
46          }
47      }
48      return   0 ;
49  }

 

  输入 1 3                    
  输出 1 2 5 8 6 3

 

 

 

 

 

 

 

 

 

 

floyd算法

弗洛伊德（Floyd）算法过程：
１、用D[v][w]记录每一对顶点的最短距离。
２、依次扫描每一个点，并以其为基点再遍历所有每一对顶点D[][]的值，看看是否可用过该基点让这对顶点间的距离更小。

算法理解：
最短距离有三种情况：
１、两点的直达距离最短。（如下图<v,x>）
２、两点间只通过一个中间点而距离最短。（图<v,u>）
３、两点间用通过两各以上的顶点而距离最短。（图<v,w>）

对于第一种情况：在初始化的时候就已经找出来了且以后也不会更改到。
对于第二种情况：弗洛伊德算法的基本操作就是对于每一对顶点，遍历所有其它顶点，看看可否通过这一个顶点让这对顶点距离更短，也就是遍历了图中所有的三角形（算法中对同一个三角形扫描了九次，原则上只用扫描三次即可，但要加入判断，效率更低）。
对于第三种情况：如下图的五边形，可先找一点（比如x，使<v,u>=2），就变成了四边形问题，再找一点（比如y,使<u,w>=2），可变成三角形问题了（v,u,w），也就变成第二种情况了，由此对于n边形也可以一步步转化成四边形三角形问题。（这里面不用担心哪个点要先找哪个点要后找，因为找了任一个点都可以使其变成（n－1）边形的问题）。

floyd的核心代码:

 

for (k=0;k<g.vexnum;k++)
{
     for (i=0;i<g.vexnum;i++)
    {
         for (j=0;j<g.vexnum;j++)
        {
             if (distance[i][j]>distance[i][k]+distance[k][j])
            {
                distance[i][j]=distance[i][k]+distance[k][j];
            }
        }
    }
}

 

结合代码 并参照上图所示 我们来模拟执行下 这样才能加深理解：
第一关键步骤：当k执行到x，i=v,j=u时，计算出v到u的最短路径要通过x，此时v、u联通了。
第二关键步骤：当k执行到u，i=v，j=y，此时计算出v到y的最短路径的最短路径为v到u，再到y(此时v到u的最短路径上一步我们已经计算过来，直接利用上步结果)。
第三关键步骤：当k执行到y时，i=v，j=w，此时计算出最短路径为v到y(此时v到y的最短路径长在第二步我们已经计算出来了)，再从y到w。

依次扫描每一点(k)，并以该点作为中介点，计算出通过k点的其他任意两点(i,j)的最短距离，这就是floyd算法的精髓！同时也解释了为什么k点这个中介点要放在最外层循环的原因.

 

// 多源最短路径,floyd_warshall算法,复杂度O(n^3)
// 求出所有点对之间的最短路经,传入图的大小和邻接阵
// 返回各点间最短距离min[]和路径pre[],pre[i][j]记录i到j最短路径上j的父结点
// 可更改路权类型,路权必须非负!
#define MAXN 200
#define inf 1000000000
typedef  int elem_t;

void floyd_warshall( int n,elem_t mat[][MAXN],elem_t min[][MAXN], int pre[][MAXN]){
     int i,j,k;
     for (i=0;i<n;i++)
         for (j=0;j<n;j++)
            min[i][j]=mat[i][j],pre[i][j]=(i==j)?-1:i;
     for (k=0;k<n;k++)
         for (i=0;i<n;i++)
             for (j=0;j<n;j++)
                 if (min[i][k]+min[k][j]<min[i][j])
                    min[i][j]=min[i][k]+min[k][j],pre[i][j]=pre[k][j];
}

本文l 来源于：http://blog.csdn.net/ll365594480/article/details/6792096