Gas Station

There are N gas stations along a circular route, where the amount of gas at station i is gas[i].

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i+1). You begin the journey with an empty tank at one of the gas stations.

Return the starting gas station's index if you can travel around the circuit once, otherwise return -1.

Note:

The solution is guaranteed to be unique.

最基本的方法：

一个个节点挨着试。。。。。

public class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int remain = 0;
        for(int i = 0 ; i < gas.length ; i ++){
            if(gas[i] > cost[i]){//如果gas[i]>cost[i],那么i就可能是start station
                remain = gas[i] - cost[i];//到下一站后的剩余油量
                for(int j = 1 ; j < gas.length;  j ++){
                    if(remain + gas[(i+j)%gas.length] > cost[(i+j)%gas.length]){//可以走到i后的第j个station
                        remain = remain + gas[(i+j)%gas.length] - cost[(i+j)%gas.length];
                        if(j == gas.length - 1){
                            return (i+j)%gas.length;
                        }
                    }else{
                        remain=0;
                        break;
                    }
                }
            }
        }
        return -1;
    }
}

Time Limit Exceeded

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i+1). You begin the journey with an 

考虑前一种算法的缺点，上述算法是一种暴力破解，需要计算每一个节点是不是start station ，而实际上，我们可以从第一个节点记录每一个的剩余油量（这样会有正有负，负的必然就不会是start station），当为正时，那么它可能就是start station，那么可以讲其设为start，然后再统计之后的节点，如果碰到某个节点之前的总剩余油量为负，那么这个节点之前的节点都不可能是start station，因此设它的下一个节点是新的start station，重新向后检测。

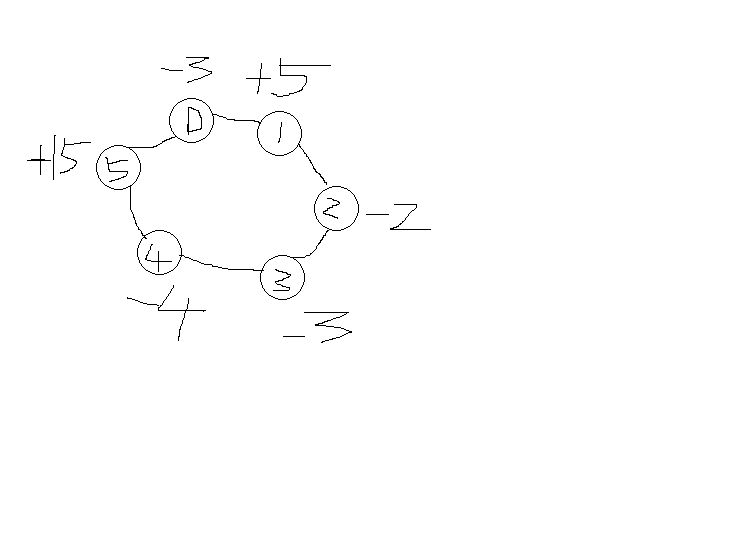
图示中，每一个节点的剩余油量如图，从0节点开始，由于未负数，故不可能是start station；而1节点的剩余油量是正值，故可能，设为start station，而到4节点时，5-2-3-4 < 0 ,因此1,2,3,4都不可能是start station。如此设5为start station。继续检测时15-3+5-2-3-4>0,故5是start station。

public class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int remain = 0;
        int start = -1;
        int pathLen = 0;//记录可能的路径长，如果pathLen == gas.length,说明可以作为一个start station
        for(int i = 0 ; i < gas.length ; i ++){
            remain = remain + gas[i] - cost[i];
            if(remain >= 0){
                pathLen ++;
                start = i;
                int count = i;
                while(pathLen < gas.length){
                    i = (i + 1) % gas.length;
                    count ++;
                    remain = remain + gas[i] - cost[i];
                    if(remain >= 0){
                        pathLen ++;
                    }else{
                        i = count;//先前的节点都不能作为start station
                        start = -1;
                        pathLen = 0;
                        remain = 0;
                        break;
                    }
                }
                if(pathLen == gas.length){
                    break;
                }
            }else{
                remain = 0;
            }
        }
        return start;
    }
}

Runtime:  363 ms

27道题了，终于独立想出一个比较好的算法了

再看别人写的，自己又，自己虽然想出来了，但是没有成为一个很系统的东西。

http://www.cnblogs.com/felixfang/p/3814463.html

public class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        //求出diff[0] 到 diff[size-1]这个非循环数组上的最大子序列MAX和最小子序列MIN，其中diff = gas - cost
        //动态规划问题
        if(gas.length == 0){
            return -1;
        }
        int max = gas[0] - cost[0];//局部最大值
        int MAX = gas[0] - cost[0];//全局最大值
        int min = gas[0] - cost[0];//局部最小值
        int MIN = gas[0] - cost[0];//全局最小值
        int stmax = 0;//局部最大值开始的位置
        int stMAX = 0;//全局最大值开始的位置
        int edMIN = 0;//全局最小值结尾的位置
        int remain = 0;
        int total = 0;
        for(int i = 0; i < gas.length; i ++){
            remain = gas[i] - cost[i];
            total += remain;
            
            if(max < 0){
                max = remain;
                stmax = i;
            }else{
                max += remain;
            }
            if(max > MAX){
                MAX = max;
                stMAX = stmax;
            }
            if(min > 0) {
                min = remain;
            }else{
                min += remain;
            } 
            if(min < MIN){
                MIN = min;
                edMIN = i; //endMIN用来存储最小序列的末尾点
            }
        }
        return total < 0 ? -1 : (MAX >= (total - MIN) ? stMAX : (edMIN+1) % gas.length);
    }
}

public class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int total = 0;
        int sum = 0;
        int start = 0;
        for(int i = 0 ; i < gas.length ; i ++){
            total += (gas[i] - cost[i]);
            if(sum < 0){
                sum = gas[i] - cost[i];
                start = i;
            }else{
                sum += gas[i] - cost[i];
            }
        }
        return total < 0 ? -1 : start ;
    }
}