平面图ST最小割（hdu 3870）

对于平面图有如下性质：

1.（欧拉公式）如果一个连通的平面图有n个点，m条边和f个面，那么f=m-n+2

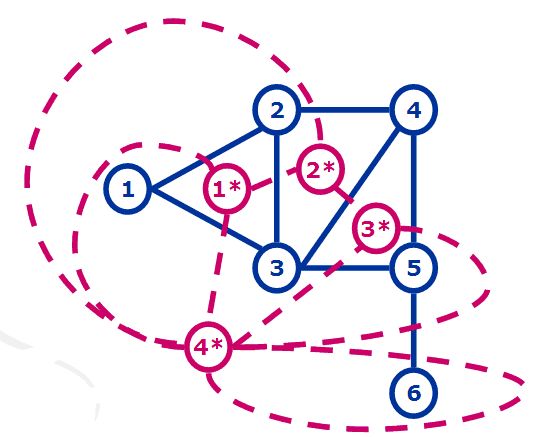
2. 每个平面图G都有一个与其对偶的平面图G*

3. G*中的每个点对应G中的一个面

4.对于G中的每条边e，e属于两个面f1、f2，加入边(f1*，f2*)。如果e只属于一个面f，加入回边(f*，f*)。

平面图G与其对偶图G*之间 关系：

1.   G的面数等于G*的点数，G*的点数等于G的面数，G与G*边数相同

2.   G*中的环对应G中的割一一对应

我们可以利用最大流—最小割定理转化模型。根据平面图与其对偶图的关系，想办法求出最小割。

对于一个s-t平面图，我们对其进行如下改造：

首先连接s-t得到一个附加面，求该图的对偶图G*，令附加面对应的点为s*，无界面对应的点为t*，然后对图G*进行连边：

因此，删掉s*到t*的边 一条从s*到t*的路径，就对应了一个s-t割，最小割的容量就等于最短路的长度 。由于平面图的偶图是稀疏图，因此最好使用堆优化的Dijkstra，可在nlogn时间内稳定求解。

参考：周冬《两极相通》

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Arrays;

public class Main{
	int maxn=160010, maxm=640010;
    long inf=1l<<50;
     class node {
         int be, ne;
         long val;
         node(int b, int e, long v) {
             be = b;
             ne = e;
             val = v;
         }
     }
     class HEAP {
         int n;
         long arr[] = new long[maxn];
         int hp[] = new int[maxn], idx[] = new int[maxn];
         // 堆数组 堆第i项是哪个元素的值 某个元素在堆中编号
         void build(long a[], int n) {
             this.n = n;
             for (int i = 1; i <= n; i++) {
                 arr[i] = a[i];
                 hp[i] = idx[i] = i;
             }
             for (int i = n / 2; i > 0; i--)                
                 heapify(i);                
         }
         void heapify(int i) {
             int l = i * 2, r = i * 2 + 1,k = i;
             if (l <= n && arr[l] < arr[k])
                 k = l;
             if (r <= n && arr[r] < arr[k])
                 k = r;
             if (k != i) {
                 swap(i, k);
                 heapify(k);
             }
         }
         void swap(int i, int j) {
             idx[hp[i]]=j;
             idx[hp[j]]=i;
             long temp=hp[i];hp[i]=hp[j];hp[j]=(int)temp;
             temp=arr[i];arr[i]=arr[j];arr[j]=temp;                
         }
         void decreasekey(int i, long v) {
             i = idx[i];
             arr[i] = v;
             while (i > 1 && arr[i] < arr[i / 2]) {
                 swap(i, i / 2);
                 i /= 2;
             }
         }
         int poll() {
             int ans = hp[1];
             idx[hp[n]] = 1;
             hp[1] = hp[n];
             arr[1] = arr[n--];
             heapify(1);
             return ans;
         }
     }
     class Dijkstra {
         int E[] = new int[maxn], len, n;
         node buf[] = new node[maxm];
         HEAP hp = new HEAP();
         void add(int a, int b, int v) {
             if(a==b)
                 return;
             buf[len] = new node(b, E[a], v);
             E[a] = len++;
             buf[len]=new node(a,E[b],v);
             E[b]=len++;
         }
         void init(int n) {
             len = 0;
             this.n = n;
             Arrays.fill(E, -1);
         }
         long d[] = new long[maxn];
         void solve(int s) {
             Arrays.fill(d, inf);
             hp.build(d, n);
             d[s]=0;
             hp.decreasekey(s, 0);
             while (hp.n > 0) {
                 int a = hp.poll();
                 for (int i = E[a]; i != -1; i = buf[i].ne) {
                     int b = buf[i].be;
                     if (d[a] + buf[i].val < d[b]){                
                         d[b]=d[a]+buf[i].val;                
                         hp.decreasekey(b, d[b]);
                     }
                 }
             }
         }
     }
 Dijkstra sp=new Dijkstra();
 StreamTokenizer in = new StreamTokenizer(new BufferedReader(
         new InputStreamReader(System.in)));
 int n,s,t;
 int nextInt() throws IOException {
     in.nextToken();
     return (int) in.nval;
 }
 int hash(int i,int j){
     if(i==0||j==n)
         return s;
     if(i==n||j==0)
         return t;
     return (i-1)*(n-1)+j;
 }
 void run() throws IOException{
     int cas=nextInt();
     while(cas-->0){
     n=nextInt();
     s=0;t=(n-1)*(n-1)+1;
     sp.init(t+1);
     for(int i=1;i<=n;i++)
         for(int j=1;j<=n;j++)
         {
             int d=nextInt();
             if(i+j==n*2)
                 continue;
             sp.add(hash(i,j)+1,hash(i-1,j)+1,d);
             sp.add(hash(i,j)+1,hash(i,j-1)+1,d);
         }
     sp.solve(1);
     System.out.println(sp.d[t+1]);
     }
 }

	public static void main(String[] args) throws IOException {
		new Main().run();
	}

}