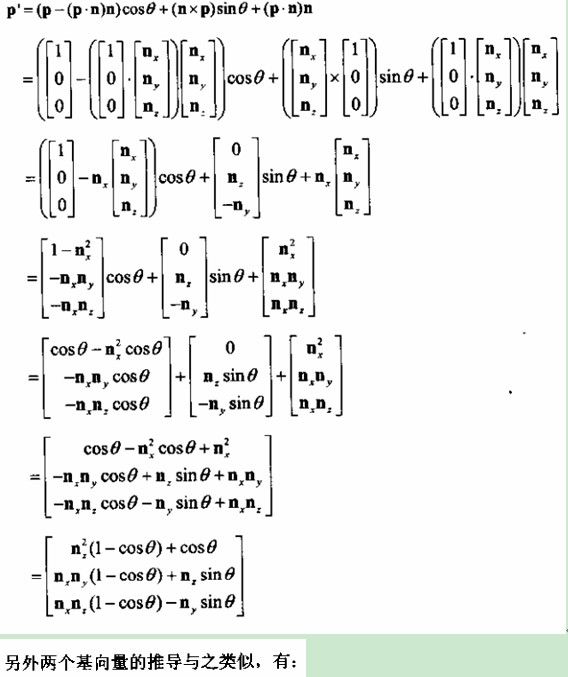
利用四元树来计算一个坐标点绕任意轴旋转后,新坐标点的推导过程
利用四元树来计算一个坐标点绕任意轴旋转后,新坐标点的推导过程(参考《(中文版)3D数学基础图形与游戏开发.pdf》):
参考源代码:
void Quaternion::setToRotateAboutAxis(const Vector3 &axis, float theta)
{
// The axis of rotation must be normalized
assert(fabs(vectorMag(axis) – 1.0f) < .01f);
// Compute the half angle and its sin
float thetaOver2 = theta * .5f;
float sinThetaOver2 = sin(thetaOver2);
// Set the values
w = cos(thetaOver2);
x = axis.x * sinThetaOver2;
y = axis.y * sinThetaOver2;
z = axis.z * sinThetaOver2;
}
最终的R(n, θ)矩阵为:
――――――
OSG中将四元树转换为矩阵(Matrix_implementation.cpp):
#define QX q._v[0]
#define QY q._v[1]
#define QZ q._v[2]
#define QW q._v[3]
void Matrix_implementation::setRotate(const Quat& q)
{
double length2 = q.length2();
。。。。。。
rlength2 = 2.0/length2;
x2 = rlength2*QX;
y2 = rlength2*QY;
z2 = rlength2*QZ;
xx = QX * x2;
xy = QX * y2;
xz = QX * z2;
yy = QY * y2;
yz = QY * z2;
zz = QZ * z2;
wx = QW * x2;
wy = QW * y2;
wz = QW * z2;
_mat[0][0] = 1.0 - (yy + zz);
_mat[1][0] = xy - wz;
_mat[2][0] = xz + wy;
_mat[0][1] = xy + wz;
_mat[1][1] = 1.0 - (xx + zz);
_mat[2][1] = yz - wx;
_mat[0][2] = xz - wy;
_mat[1][2] = yz + wx;
_mat[2][2] = 1.0 - (xx + yy);
}
――――――
3.从矩阵转换到四元树:
OSG中将矩阵转换为四元树(Matrix_implementation.cpp):
#define QX q._v[0]
#define QY q._v[1]
#define QZ q._v[2]
#define QW q._v[3]
Quat Matrix_implementation::getRotate() const
{
Quat q;
value_type s;
value_type tq[4];
int i, j;
// Use tq to store the largest trace
tq[0] = 1 + _mat[0][0]+_mat[1][1]+_mat[2][2];
tq[1] = 1 + _mat[0][0]-_mat[1][1]-_mat[2][2];
tq[2] = 1 - _mat[0][0]+_mat[1][1]-_mat[2][2];
tq[3] = 1 - _mat[0][0]-_mat[1][1]+_mat[2][2];
// 找4个中最大的
j = 0;
for(i=1;i<4;i++) j = (tq[i]>tq[j])? i : j;
// check the diagonal
if (j==0)
{
/* perform instant calculation */
QW = tq[0];
QX = _mat[1][2]-_mat[2][1];
QY = _mat[2][0]-_mat[0][2];
QZ = _mat[0][1]-_mat[1][0];
}
else if (j==1)
{
QW = _mat[1][2]-_mat[2][1];
QX = tq[1];
QY = _mat[0][1]+_mat[1][0];
QZ = _mat[2][0]+_mat[0][2];
}
else if (j==2)
{
QW = _mat[2][0]-_mat[0][2];
QX = _mat[0][1]+_mat[1][0];
QY = tq[2];
QZ = _mat[1][2]+_mat[2][1];
}
else /* if (j==3) */
{
QW = _mat[0][1]-_mat[1][0];
QX = _mat[2][0]+_mat[0][2];
QY = _mat[1][2]+_mat[2][1];
QZ = tq[3];
}
s = sqrt(0.25/tq[j]);
QW *= s;
QX *= s;
QY *= s;
QZ *= s;
return q;
}