《最优化方法及其Matlab程序设计》马昌凤 部分习题答案
第12章 序列二次规划法
6.用SQP方法的Matlab程序求解下列优化问题:
(1)
%%% 目标函数 f(x) %%%%%%%%%%% function f=f1(x) % f=-pi*x(1)^2*x(2); f = (x(1)-2)^4 + (x(1)-2*x(2))^2; %%%% 目标函数 f(x) 的梯度%%%%% function df=df1(x) % df=[-2*pi*x(1)*x(2), -pi*x(1)^2]'; df = [4*(x(1)-2)^3+2*(x(1)-2*x(2)); -4*(x(1)-2*x(2))]; %%%% 约束函数 %%%%%% function [h,g]=cons(x) % h=[pi*x(1)*x(2)+pi*x(1)^2-150]; h=[]; % g=[x(1);x(2)]; g = [x(1)^2 + x(2)]; %% 约束函数 Jacobi矩阵%%%% function [dh,dg]=dcons(x) % dh=[pi*x(2)+2*pi*x(1), pi*x(1)]; dh = []; % dg=[1 0; 0 1]; dg = [2*x(1), 1];
调用:
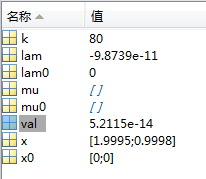
x0 = [0 0]'; mu0 = [ ]; lam0 = [0]; [x,mu,lam,val,k] = sqpm(x0,mu0,lam0);结果
(2)
%%% 目标函数 f(x) %%%%%%%%%%% function f=f1(x) % f=-pi*x(1)^2*x(2); % f = (x(1)-2)^4 + (x(1)-2*x(2))^2; s = -x(1)-x(2); f = exp(s) + x(1)^2 + 2*x(1)*x(2) + x(2)^2 + 2*x(1) + 6*x(2);
%%%% 目标函数 f(x) 的梯度%%%%% function df=df1(x) s = -x(1)-x(2); df = [-exp(s)+2*x(1)+2*x(2)+2; -exp(s)+2*x(1)+2*x(2)+6];
%%%% 约束函数 %%%%%% function [h,g]=cons(x) % h=[pi*x(1)*x(2)+pi*x(1)^2-150]; h=[]; g = [2-x(1)-x(2),x(1),x(2)];
%% 约束函数 Jacobi矩阵%%%% function [dh,dg]=dcons(x) % dh=[pi*x(2)+2*pi*x(1), pi*x(1)]; dh = []; dg = [-1 -1;1 0;0 1];
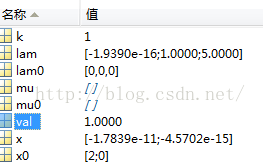
x0 = [2 0]'; mu0 = [ ]; lam0 = [0 0 0]; [x,mu,lam,val,k] = sqpm(x0,mu0,lam0);
结果