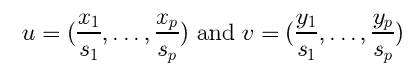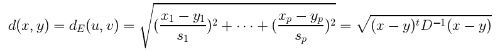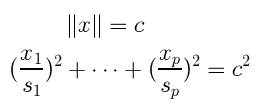马氏距离(mahalanobis)

定义：p维空间的两点（两个p维向量x,y）的距离定义为：

 并且点x欧氏模数为：

这里很快可以得出，所有到原点距离相等的点满足

这是某个正球体的方程。这就是说观测数据x的各个分量对x至中心的欧式距离贡献是相等的。然而在统计学中我们希望寻求这样一种距离，它的各个分量的作用程度是不同的。差别较大的分量应该接受较小的权重。

如

然后定义x,y之间的距离

这里

现在x的模数等于

所有到原点等距离的点满足

这是以原点为中心的某个椭球体的方程。

=========================================================================================

马氏距离是由印度统计学家马哈拉诺比斯（P. C. Mahalanobis）提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的（scale-invariant），即独立于测量尺度。 对于一个均值为，协方差矩阵为的多变量矢量，其马氏距离为

马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为的随机变量与的差异程度：

如果协方差矩阵为单位矩阵，马氏距离就简化为欧式距离；如果协方差矩阵为对角阵，其也可称为正规化的马氏距离。

其中是的标准差。