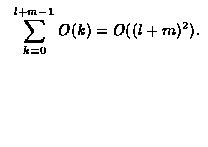数据结构之“Ordered List and Sorted List”(七)
本文主要学习“Sorted List”的应用—— 多项式相加(the addition of two polynomials,点击打开链接)。
一、多项式相加的计算机表示
前面学习“Ordered List”的应用的时候,我们学到用“a sequence of ordered pairs”来表示一个多项式。如下:
然后,用“Ordered List”来表示这个多项式,并编写了一个算法来求该多项式的微分。(点击打开链接)
在计算多项式的微分的算法中,多项式中的每一项在序列中的具体位置并不影响该算法的效率。但是,如果我们考虑两个多项式相加的算法:它需要找出指数(exponent)相同的项,即分组(group),然将指数相同的项的系数(coefficient)相加。如果多项式中的项的位置是任意的,这个分组的过程需要多次遍历“Ordered List”,效率非常低。反之,如果多项式的项是从小到大(按指数)排列的,那么这个分组仅需一次遍历。
二、实现
接口声明:
#pragma once
#include "SortedListAsLinkedList.h"
// the oredered pair
class TermB : public Object
{
public:
TermB(double, unsigned int);
void Put(std::ostream &)const;
void Differentiate();
double Coefficient() const;
unsigned int Exponent() const;
friend TermB operator+(const TermB&, const TermB&);
protected:
int CompareTo(Object const &) const;
private:
double coefficient;
unsigned int exponent;
};
class SortedPolynomial : public SortedListAsLinkedList
{
public:
SortedPolynomial();
~SortedPolynomial();
SortedPolynomial(SortedPolynomial&);
friend SortedPolynomial operator+(const SortedPolynomial &, const SortedPolynomial &);
};
实现
#include "stdafx.h"
#include "SortedPolynomial.h"
TermB::TermB(double _coefficient, unsigned int _exponent)
: coefficient(_coefficient)
, exponent(_exponent)
{
}
void TermB::Put(std::ostream & s) const
{
s << typeid(*this).name() << " {";
s << coefficient << "," << exponent;
s << " }";
}
void TermB::Differentiate()
{
if (exponent > 0)
{
coefficient *= exponent;
--exponent;
}
else
coefficient = 0;
}
double TermB::Coefficient() const
{
return coefficient;
}
unsigned int TermB::Exponent() const
{
return exponent;
}
TermB operator+(const TermB& arg1, const TermB& arg2)
{
if (arg1.exponent != arg2.exponent)
throw std::domain_error("unequal exponent");
return TermB(arg1.coefficient + arg2.coefficient, arg1.exponent);
}
int TermB::CompareTo(Object const & object) const
{
TermB const & term = dynamic_cast<TermB const &> (object);
if (exponent == term.exponent)
return ::Compare(coefficient, term.coefficient);
else
return exponent - term.exponent;
}
SortedPolynomial::SortedPolynomial()
{
}
SortedPolynomial::~SortedPolynomial()
{
}
SortedPolynomial::SortedPolynomial(SortedPolynomial& arg)
{
Purge();
Pos & pos = *new Pos(arg, arg.linkedList.Head());
//Iterator & pos = arg.NewIterator();
while (!pos.IsDone())
{
const TermB & term = dynamic_cast<const TermB &> (*pos);
Insert(*new TermB(term));
++pos;
}
}
SortedPolynomial operator+(const SortedPolynomial & arg1, const SortedPolynomial & arg2)
{
SortedPolynomial result;
ListAsLinkedList::Pos & pos1 = *new ListAsLinkedList::Pos(arg1, arg1.linkedList.Head());
ListAsLinkedList::Pos & pos2 = *new ListAsLinkedList::Pos(arg2, arg2.linkedList.Head());
//Iterator & pos1 = arg1.NewIterator();
//Iterator & pos2 = arg2.NewIterator();
while (!pos1.IsDone() && !pos2.IsDone())
{
const TermB & term1 = dynamic_cast<const TermB &> (*pos1);
const TermB & term2 = dynamic_cast<const TermB &> (*pos2);
if (term1.Exponent() < term2.Exponent())
{
result.Insert(*new TermB(term1));
++pos1;
}
else if (term1.Exponent() > term2.Exponent())
{
result.Insert(*new TermB(term2));
++pos2;
}
else
{
TermB sum = term1 + term2;
if (sum.Coefficient())
result.Insert(*new TermB(sum));
++pos1;
++pos2;
}
}
while (!pos1.IsDone())
{
const TermB & term1 = dynamic_cast<const TermB &> (*pos1);
result.Insert(*new TermB(term1));
++pos1;
}
while (!pos2.IsDone())
{
const TermB & term2 = dynamic_cast<const TermB &> (*pos2);
result.Insert(*new TermB(term2));
++pos2;
}
delete& pos1;
delete& pos2;
return result;
}
三、测试
测试代码
// test for Polynomial Addition
{
SortedPolynomial polynomial;
TermB pArray[] = { TermB(5,0), TermB(32,5), TermB(4,2), TermB(56,3), TermB(16,4), TermB(45,1) };
for (unsigned int i = 0; i < 6; ++i)
polynomial.Insert(pArray[i]);
polynomial.Put(std::cout);
cout << endl;
SortedPolynomial polynomial2;
TermB pArray2[] = { TermB(5, 0), TermB(32, 5), TermB(4, 2), TermB(56, 3), TermB(16, 4), TermB(45, 6) };
for (unsigned int i = 0; i < 6; ++i)
polynomial2.Insert(pArray2[i]);
polynomial2.Put(std::cout);
cout << endl;
SortedPolynomial polynomial3 = polynomial + polynomial2;
polynomial3.Put(std::cout);
polynomial.RescindOwnership();
polynomial2.RescindOwnership();
polynomial3.RescindOwnership();
}
四、分析和优化
1,“互补多项式”求和
假设计算两个“互补多项式”(a addition of a polynomial and its arithmetic complement)的和。这两个多项式对应项相加为0,最终结果也为零,即在求和函数中无需执行“Insert”。那么它的总消耗时间就是主循环的次数,即O(n)。
注:先考虑特殊情况,再考虑一般情况,这是一种解决问题的思路。
2,一般多项求和
假设两个项数不相等的多项式,p(x) < q(x)。主循环执行L次,次循环执行M次。“Insert”函数为O(k),则求和函数的效率为:
最坏的情况是O(n*n)。主要是因为,我们在分析时假设“Insert”函数不知道每次的具体插入位置。事实上,在循环中,每次都是“在尾部插入”,参照“Insert”函数的实现:
void SortedListAsLinkedList::Insert(Object & object)
{
const Node<Object*>* prevPtr = NULL;
const Node<Object*>* ptr = linkedList.Head();
while (ptr != NULL && *ptr->Datum() < object)
{
prevPtr = ptr;
ptr = ptr->Next();
}
if (!prevPtr)
linkedList.Prepend(&object);
else
linkedList.InsertAfter(prevPtr, &object);
++count;
}
我们可以进行以下优化,取代Insert。
SortedPolynomial operator+(const SortedPolynomial & arg1, const SortedPolynomial & arg2)
{
SortedPolynomial result;
ListAsLinkedList::Pos & pos1 = *new ListAsLinkedList::Pos(arg1, arg1.linkedList.Head());
ListAsLinkedList::Pos & pos2 = *new ListAsLinkedList::Pos(arg2, arg2.linkedList.Head());
//Iterator & pos1 = arg1.NewIterator();
//Iterator & pos2 = arg2.NewIterator();
while (!pos1.IsDone() && !pos2.IsDone())
{
const TermB & term1 = dynamic_cast<const TermB &> (*pos1);
const TermB & term2 = dynamic_cast<const TermB &> (*pos2);
if (term1.Exponent() < term2.Exponent())
{
result.linkedList.Append(new TermB(term1));// result.Insert(*new TermB(term1));
++pos1;
}
else if (term1.Exponent() > term2.Exponent())
{
result.linkedList.Append(new TermB(term2)); //result.Insert(*new TermB(term2));
++pos2;
}
else
{
TermB sum = term1 + term2;
if (sum.Coefficient())
result.linkedList.Append(new TermB(sum)); // result.Insert(*new TermB(sum));
++pos1;
++pos2;
}
}
while (!pos1.IsDone())
{
const TermB & term1 = dynamic_cast<const TermB &> (*pos1);
result.linkedList.Append(new TermB(term1)); // result.Insert(*new TermB(term1));
++pos1;
}
while (!pos2.IsDone())
{
const TermB & term2 = dynamic_cast<const TermB &> (*pos2);
result.linkedList.Append(new TermB(term2)); // result.Insert(*new TermB(term2));
++pos2;
}
delete& pos1;
delete& pos2;
return result;
}
优化后,运行时间降为O(n)。