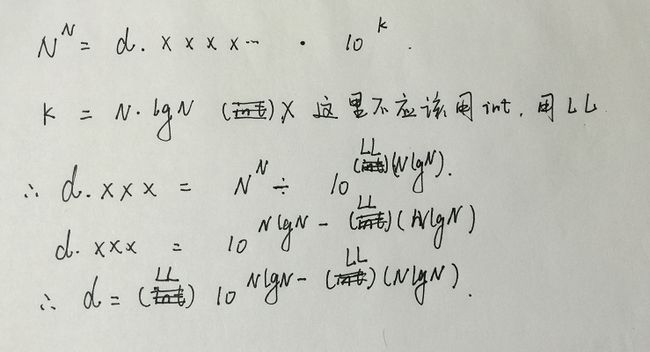NEFU 65 , HDU 1060, POJ 2109
关于指数对数运算的一些问题
数的长度
Problem:65
Time Limit:1000ms
Memory Limit:65536K
Description
N! (N的阶乘) 是非常大的数,计算公式为:N! = N * (N - 1) * (N - 2) * ... * 2 * 1)。现在需要知道N!有多少(十进制)位。
Input
每行输入1个正整数N。0 < N < 1000000
Output
对于每个N,输出N!的(十进制)位数。
Sample Input
1 3 32000 1000000
Sample Output
1 1 130271 5565709
1、log(n)是n对2取对数log10(n)才是对10取对数
2、N!的位数是lg(1) + .... + lg(N) ,最终再向下取整加一
3、不要这样做 : (int)log10(i) 其中i 从1到n。这样不对,不信你输入一个4试试,结果绝对是1
代码:/*
* test.cpp
*
* Created on: 2016年3月12日
* Author: Triose
*/
#include<stdio.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<iterator>
#include<math.h>
#include<stdlib.h>
#include<map>
#include<set>
using namespace std;
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff
#define inf 0x3f3f3f3f
#define rep(i,a) for((i)=0; i<(a);(i)++)
#define mem(a,b) (memset((a),b,sizeof(a)))
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define sfs(a) scanf("%s",a)
#define pf(a) printf("%d\n",a)
#define pfs(a) printf("%s\n",a)
#define pfI(a) printf("%I64d\n",a)
#define LL __int64
const double PI = acos(-1.0);
template<class T> T gcd(T a, T b) { return b ? gcd(b, a%b) : a; }
template<class T> T lcm(T a, T b) { return a / gcd(a, b)*b; }
template<class T> inline T Min(T a, T b) { return a<b ? a : b; }
template<class T> inline T Max(T a, T b) { return a>b ? a : b; }
int n, m;
int main() {
while(sf(n) != EOF) {
double ans = 1;
for(int i = 1; i <= n; i++) {
ans += log10(i * 1.0);
}
pf((int)ans);
}
return 0;
}
一道水题啦,长长记性
其实还有另一道看上去一头雾水的题目(因为我弱嘛),后来看着看着做发现是这么回事。。。以后做题的时候一定不能再看书了!
Leftmost Digit
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 15705 Accepted Submission(s): 6113
Problem Description
Given a positive integer N, you should output the leftmost digit of N^N.
Input
The input contains several test cases. The first line of the input is a single integer T which is the number of test cases. T test cases follow.
Each test case contains a single positive integer N(1<=N<=1,000,000,000).
Each test case contains a single positive integer N(1<=N<=1,000,000,000).
Output
For each test case, you should output the leftmost digit of N^N.
Sample Input
2 3 4
Sample Output
2 2HintIn the first case, 3 * 3 * 3 = 27, so the leftmost digit is 2. In the second case, 4 * 4 * 4 * 4 = 256, so the leftmost digit is 2.
代码:
/*
* test.cpp
*
* Created on: 2016年3月12日
* Author: Triose
*/
#include<stdio.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<iterator>
#include<math.h>
#include<stdlib.h>
#include<map>
#include<set>
using namespace std;
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff
#define inf 0x3f3f3f3f
#define rep(i,a) for((i)=0; i<(a);(i)++)
#define mem(a,b) (memset((a),b,sizeof(a)))
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define sfs(a) scanf("%s",a)
#define pf(a) printf("%d\n",a)
#define pfs(a) printf("%s\n",a)
#define pfI(a) printf("%I64d\n",a)
#define LL __int64
const double PI = acos(-1.0);
template<class T> T gcd(T a, T b) { return b ? gcd(b, a%b) : a; }
template<class T> T lcm(T a, T b) { return a / gcd(a, b)*b; }
template<class T> inline T Min(T a, T b) { return a<b ? a : b; }
template<class T> inline T Max(T a, T b) { return a>b ? a : b; }
LL n, m;
int main() {
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
// freopen("Out.txt", "w", stdout);
#endif
int t;
sf(t);
while(t--) {
sfI(n);
double k1 = n * log10(n * 1.0);
k1 -= (LL) k1;
pfI((LL)pow(10.0, k1));
}
return 0;
}
神奇的取对数和double类型。。。
Power of Cryptography
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 21825 | Accepted: 11033 |
Description
Current work in cryptography involves (among other things) large prime numbers and computing powers of numbers among these primes. Work in this area has resulted in the practical use of results from number theory and other branches of mathematics once considered to be only of theoretical interest.
This problem involves the efficient computation of integer roots of numbers.
Given an integer n>=1 and an integer p>= 1 you have to write a program that determines the n th positive root of p. In this problem, given such integers n and p, p will always be of the form k to the n th. power, for an integer k (this integer is what your program must find).
This problem involves the efficient computation of integer roots of numbers.
Given an integer n>=1 and an integer p>= 1 you have to write a program that determines the n th positive root of p. In this problem, given such integers n and p, p will always be of the form k to the n th. power, for an integer k (this integer is what your program must find).
Input
The input consists of a sequence of integer pairs n and p with each integer on a line by itself. For all such pairs 1<=n<= 200, 1<=p<10
101 and there exists an integer k, 1<=k<=10
9 such that k
n = p.
Output
For each integer pair n and p the value k should be printed, i.e., the number k such that k n =p.
Sample Input
2 16 3 27 7 4357186184021382204544
Sample Output
4 3 1234
题目意思是:给你n,p让你求k,使得k^n = p;
这道题目两种做法:
一:大整数乘法+二分
以样例三为例,根据n和p的关系是可以确定出k的位数的,例如:n=7,p=4357186184021382204544,p的位数为22,用22/7的结果向上取整,得到4,即为k的位数,也就是说k的取值范围是1000~9999。在这个范围内进行二分查找,就可以找到满足条件的k值。(这一段是复制了别人的)。
二、直接double类型 然后 cout pow(p,1 / n)
记住一定要用cout 因为printf 过不了。。。
#include<stdio.h>
#include<iostream>
#include<string>
#include<string.h>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<iterator>
#include<math.h>
#include<stdlib.h>
#include<map>
#include<set>
using namespace std;
//#define ONLINE_JUDGE
#define eps 1e-8
#define INF 0x7fffffff
#define inf 0x3f3f3f3f
#define rep(i,a) for((i)=0; i<(a);(i)++)
#define mem(a,b) (memset((a),b,sizeof(a)))
#define sf(a) scanf("%d",&a)
#define sfI(a) scanf("%I64d",&a)
#define sfd(a,b) scanf("%d%d",&a,&b)
#define sft(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define sfs(a) scanf("%s",a)
#define pf(a) printf("%d\n",a)
#define pfs(a) printf("%s\n",a)
#define pfI(a) printf("%I64d\n",a)
#define LL __int64
const double PI = acos(-1.0);
template<class T> T gcd(T a, T b) { return b ? gcd(b, a%b) : a; }
template<class T> T lcm(T a, T b) { return a / gcd(a, b)*b; }
template<class T> inline T Min(T a, T b) { return a<b ? a : b; }
template<class T> inline T Max(T a, T b) { return a>b ? a : b; }
double n, m;
int main() {
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
// freopen("Out.txt", "w", stdout);
#endif
while(cin >> n >> m) {
cout << pow(m,1 / n) << endl;
}
return 0;
}