线段树求矩形面积并 方法详解 (扫描线)HDU 1542 & HDU 3265 & POJ 1151
原文链接:
http://www.cnblogs.com/scau20110726/archive/2013/03/21/2972808.html
http://www.cnblogs.com/Booble/archive/2010/10/10/1847163.html
http://www.cnblogs.com/fenshen371/p/3214092.html
http://www.cnblogs.com/qq1012662902/p/3859063.html
这两篇是我迄今为止发现的几篇讲解扫描线最形象最详细的!
第一篇:
hdu 1542 Atlantis
线段树求矩形面积并
经典题目,poj 1151 是相同的题目。终于学了求矩形面积并,详细说一下。
首先是看小hh的线段树专题,因为找不到什么论文来看所以只好啃他的代码,啃了一个晚上,有感觉,但是不确定,只能轻轻体会到扫描线的意义。后来啃不下去了,就自己想,给想了出来,但是想出来居然是跟原始的方法不同的。所以下面说的是原始的方法(或者说是小hh代码中的方法),以及我自己想出来的一种方法,两种虽然不同,但是个人感觉本质还是差不多的,不过从效率上看,小hh的那种代码应该效率更高。另外下面给出的代码都是用线段树来模拟扫描法,其实还有更好的方法就是用DP的思想去优化,据说效率提高不是一点两点而是很多,但是还没学,学完会继续更新
分析:
1.矩形比较多,坐标也很大,所以横坐标需要离散化(纵坐标不需要),熟悉离散化后这个步骤不难,所以这里不详细讲解了,不明白的还请百度
2.重点:扫描线法:假想有一条扫描线,从左往右(从右往左),或者从下往上(从上往下)扫描过整个多边形(或者说畸形。。多个矩形叠加后的那个图形)。如果是竖直方向上扫描,则是离散化横坐标,如果是水平方向上扫描,则是离散化纵坐标。下面的分析都是离散化横坐标的,并且从下往上扫描的。
扫描之前还需要做一个工作,就是保存好所有矩形的上下边,并且按照它们所处的高度进行排序,另外如果是上边我们给他一个值-1,下边给他一个值1,我们用一个结构体来保存所有的上下边
struct segment
{
double l,r,h; //l,r表示这条上下边的左右坐标,h是这条边所处的高度
int f; //所赋的值,1或-1
}
接着扫描线从下往上扫描,每遇到一条上下边就停下来,将这条线段投影到总区间上(总区间就是整个多边形横跨的长度),这个投影对应的其实是个插入和删除线段操作。还记得给他们赋的值1或-1吗,下边是1,扫描到下边的话相当于往总区间插入一条线段,上边-1,扫描到上边相当于在总区间删除一条线段(如果说插入删除比较抽象,那么就直白说,扫描到下边,投影到总区间,对应的那一段的值都要增1,扫描到上边对应的那一段的值都要减1,如果总区间某一段的值为0,说明其实没有线段覆盖到它,为正数则有,那会不会为负数呢?是不可能的,可以自己思考一下)。
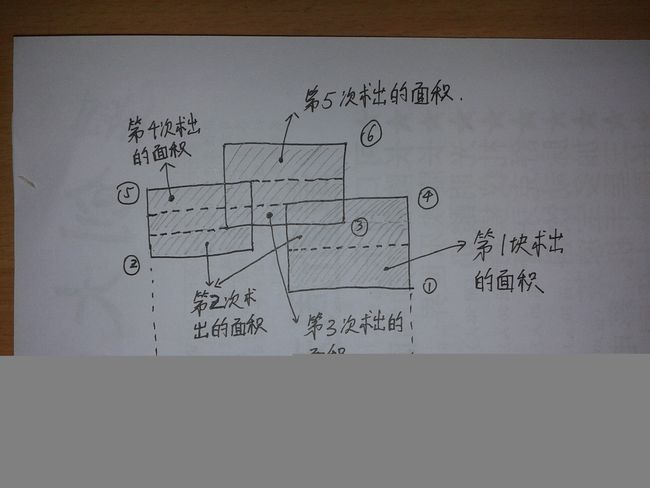
每扫描到一条上下边后并投影到总区间后,就判断总区间现在被覆盖的总长度,然后用下一条边的高度减去当前这条边的高度,乘上总区间被覆盖的长度,就能得到一块面积,并依此做下去,就能得到最后的面积
(这个过程其实一点都不难,只是看文字较难体会,建议纸上画图,一画即可明白,下面献上一图希望有帮组)
从这个图,也可以感受到,就好比一个畸形的容器,往里面倒水,从最下面往上面涨,被水淹过的部分其实就是我们要求的面积
下面给出代码(离散化)
/*
1.保存矩形的上下边界,并且重要的,记录他们是属于上还是下,然后按高度升序排序
2.保存竖线坐标,并且去重,是为了离散化
3.以保存的上下边界数组去更新
*/
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define INF 0x3f3f3f3f
#define MAX 110
#define LL rt*2
#define RR rt*2+1
struct segment //保存矩形上下边界
{
double l,r,h; //左右横坐标,纵坐标
int f; //-1为下边界,1为上边界
} ss[2*MAX];
struct node //线段树节点
{
int l,r;
int cover; //该节点被覆盖的情况
double len; //该区间被覆盖的总长度
} tt[2*MAX*4];
double pos[2*MAX];
int nums;
int cmp(struct segment a ,struct segment b)
{
return a.h < b.h;
}
void build(int a, int b ,int rt)
{
tt[rt].l = a;
tt[rt].r = b;
tt[rt].cover = 0;
tt[rt].len = 0;
if(a == b)
return ;
int mid = (tt[rt].l+tt[rt].r)/2;
build(a,mid,LL);
build(mid+1,b,RR);
}
int binary(double key ,int low, int high)
{
while(low <= high)
{
int mid = (low+high)>>1;
if(pos[mid] == key)
return mid;
else if(key < pos[mid])
high = mid-1;
else
low = mid+1;
}
return -1;
}
void pushup(int rt)
{
if(tt[rt].cover) //非0,已经被整段覆盖
tt[rt].len = pos[tt[rt].r+1] - pos[tt[rt].l];
else if(tt[rt].l == tt[rt].r) //已经不是一条线段
tt[rt].len = 0;
else //是一条线段但是又没有整段覆盖,那么只能从左右孩子的信息中获取
tt[rt].len = tt[LL].len + tt[RR].len ;
}
void update(int a, int b ,int val ,int rt)
{
if(tt[rt].l==a && tt[rt].r==b) //目标区间
{
tt[rt].cover += val; //更新这个区间被覆盖的情况,//插入或删除操作直接让cover[]+=flag。当cover[]>0时,该区间一定有边覆盖。
pushup(rt); //更新这个区间被覆盖的总长度
return ;
}
int mid = (tt[rt].l+tt[rt].r)/2;
if(b <= mid) //只访问左孩子
update(a,b,val,LL);
else if(a > mid) //只访问有孩子
update(a,b,val,RR);
else //左右都要访问
{
update(a,mid,val,LL);
update(mid+1,b,val,RR);
}
pushup(rt); //计算该区间被覆盖的总长度
}
int main()
{
int Case = 0;
int n;
double x1, y1, x2, y2;
while(scanf("%d",&n)!=EOF && n)
{
nums=0;
for(int i = 0; i < n; i++)
{
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
ss[nums].l = x1;
ss[nums].r = x2;
ss[nums].h = y1;
ss[nums].f = 1;
//记录下边界的信息
ss[nums+1].l = x1;
ss[nums+1].r = x2;
ss[nums+1].h = y2;
ss[nums+1].f = -1;
//记录上边界的信息
pos[nums] = x1;
pos[nums+1] = x2;
//记录横坐标
nums += 2;
}
sort(ss,ss+nums,cmp); //横线 按纵坐标(高度)升序排序
sort(pos,pos+nums); //横坐标 升序排序,离散化
// for(int i = 0; i < nums; i++)
// printf("%.2lf %.2lf %.2lf\n",ss[i].l,ss[i].r,ss[i].h);
int m = 1;
for(int i = 1; i < nums; i++)
if(pos[i] != pos[i-1]) //去重,为了离散化
pos[m++] = pos[i];
build(0, m-1, 1); //离散化后的区间就是[0,m-1],以此建树
double ans = 0;
for(int i = 0; i < nums; i++) //拿出每条横线并且更新
{
int l = binary(ss[i].l,0,m-1);
int r = binary(ss[i].r,0,m-1)-1;
update(l,r,ss[i].f,1); //用这条线段去更新//每插入一次就算一次 ,相对应的边在线段树中会抵消
ans += (ss[i+1].h-ss[i].h)*tt[1].len;//高 X 低
//printf("%.2lf\n",ans);
}
printf("Test case #%d\n",++Case);
printf("Total explored area: %.2f\n\n",ans);
}
return 0;
}
第二篇:
POJ 1151 Atlantis 线段树求矩形面积并 方法详解
第一次做线段树扫描法的题,网搜各种讲解,发现大多数都讲得太过简洁,不是太容易理解。所以自己打算写一个详细的。看完必会o(∩_∩)o
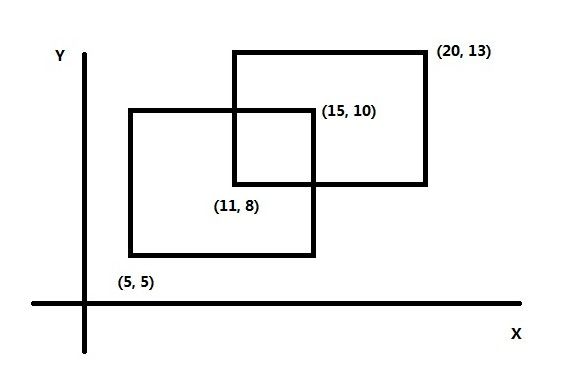
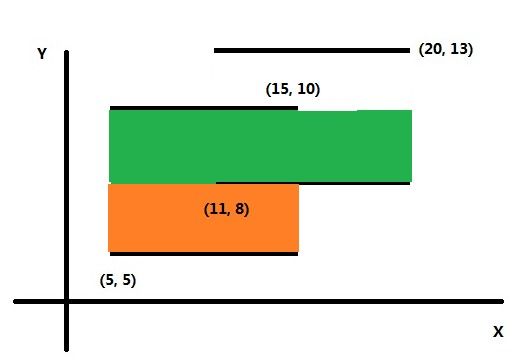
顾名思义,扫描法就是用一根想象中的线扫过所有矩形,在写代码的过程中,这根线很重要。方向的话,可以左右扫,也可以上下扫。方法是一样的,这里我用的是由下向上的扫描法。
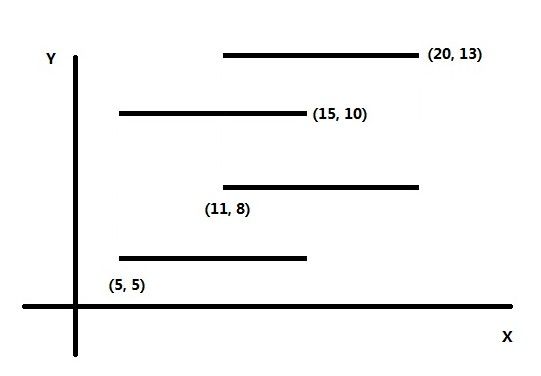
如上图所示,坐标系内有两个矩形。位置分别由左下角和右上角顶点的坐标来给出。上下扫描法是对x轴建立线段树,矩形与y平行的两条边是没有用的,在这里直接去掉。如下图。
现想象有一条线从最下面的边开始依次向上扫描。线段树用来维护当前覆盖在x轴上的线段的总长度,初始时总长度为0。用ret来保存矩形面积总和,初始时为0。
由下往上扫描,扫描到矩形的底边时将它插入线段树,扫描到矩形的顶边时将底边从线段树中删除。而在代码中实现的方法就是,每条边都有一个flag变量,底边为1,顶边为-1。
用cover数组(通过线段树维护)来表示某x轴坐标区间内是否有边覆盖,初始时全部为0。插入或删除操作直接让cover[] += flag。当cover[] > 0 时,该区间一定有边覆盖。
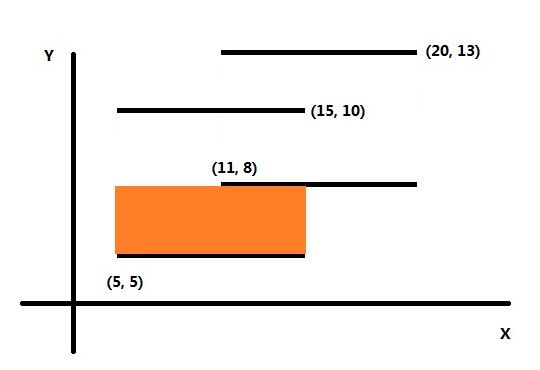
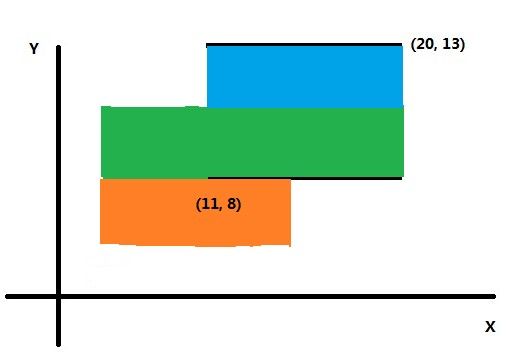
开始扫描到第一条线,将它压入线段树,此时覆盖在x轴上的线段的总长度L为10。计算一下它与下一条将被扫描到的边的距离S(即两条线段的纵坐标之差,该例子里此时为3)。
则 ret += L * S. (例子里增量为10*3=30)
结果如下图
扫描到第二条边,将它压入线段树,计算出此时覆盖在x轴上的边的总长度。
例子里此时L=15。与下一条将被扫描到的边的距离S=2。 ret += 30。 如下图所示。
接下来扫描到了下方矩形的顶边,从线段树中删除该矩形的底边,并计算接下来面积的增量。如下图。
此时矩形覆盖的总面积已经计算完成。 可以看到,当共有n条底边和顶边时,只需要从下往上扫描n-1条边即可计算出总面积。
============================== 分割线 ========================================
此题因为横坐标包含浮点数,因此先离散化。另外,因为用线段树维护的是覆盖在x轴上的边,而边是连续的,并非是一个个断点,因此线段树的每一个叶子结点实际存储的是该点与下一点之间的距离。代码中r+1, r-1的地方多多体会。代码我是看着HH大神的代码写的,基本一样。在这里膜拜一下。。。
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define maxn 222
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
using namespace std;
int cover[maxn<<2];
double sum[maxn<<2], x[maxn];
struct seg
{
double l, r, h;
int flag;
seg() {}
seg(double a,double b,double c,int d) : l(a), r(b), h(c), flag(d) {}
bool operator < (const seg &cmp) const
{
return h < cmp.h;
}
}ss[maxn];
int bin(double key, int len, double x[])
{
int l = 0, r = len - 1;
while (l <= r)
{
int m = (l + r) >> 1;
if (key == x[m]) return m;
else if (key < x[m]) r = m - 1;
else l = m + 1;
}
return -1;
}
void PushUp(int rt,int l,int r)
{
if (cover[rt]) sum[rt] = x[r+1] - x[l];
else if (l == r) sum[rt] = 0;
else sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
void update(int L,int R,int f,int l,int r,int rt)
{
if (L <= l && r <= R)
{
cover[rt] += f;
PushUp(rt, l, r);
return;
}
int m = (l + r) >> 1;
if (L <= m) update(L, R, f, lson);
if (m < R) update(L, R, f, rson);
PushUp(rt, l, r);
}
int main()
{
int n;
int cas = 1;
//freopen("data.in","r",stdin);
while (~scanf("%d",&n) && n)
{
int m = 0;
for (int i = 0; i < n; i++)
{
double x1,y1,x2,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
x[m] = x1;
ss[m++] = seg(x1, x2, y1, 1);
x[m] = x2;
ss[m++] = seg(x1, x2, y2, -1);
}
sort(x, x + m);
sort(ss, ss + m);
int k = 1;
for (int i = 1; i < m; i++)
if (x[i] != x[i-1]) x[k++] = x[i];
memset(cover, 0, sizeof(cover));
memset(sum, 0, sizeof(sum));
double ret = 0;
for (int i = 0; i < m - 1; i++)
{
int l = bin(ss[i].l, k, x);
int r = bin(ss[i].r, k, x) - 1;
if (l <= r) update(l, r, ss[i].flag, 0, k - 1, 1);
ret += sum[1] * (ss[i+1].h - ss[i].h);
}
printf("Test case #%d\nTotal explored area: %.2lf\n\n",cas++,ret);
}
return 0;
}
第三篇:
HDU 3265 扫描线+线段树
Posters
Time Limit: 5000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4380 Accepted Submission(s): 971
However, Ted is such a picky guy that in every poster he finds something ugly. So before he pastes a poster on the window, he cuts a rectangular hole on that poster to remove the ugly part. Ted is also a careless guy so that some of the pasted posters may overlap when he pastes them on the window.
Ted wants to know the total area of the window covered by posters. Now it is your job to figure it out.
To make your job easier, we assume that the window is a rectangle located in a rectangular coordinate system. The window’s bottom-left corner is at position (0, 0) and top-right corner is at position (50000, 50000). The edges of the window, the edges of the posters and the edges of the holes on the posters are all parallel with the coordinate axes.
The input ends with a line of single zero.
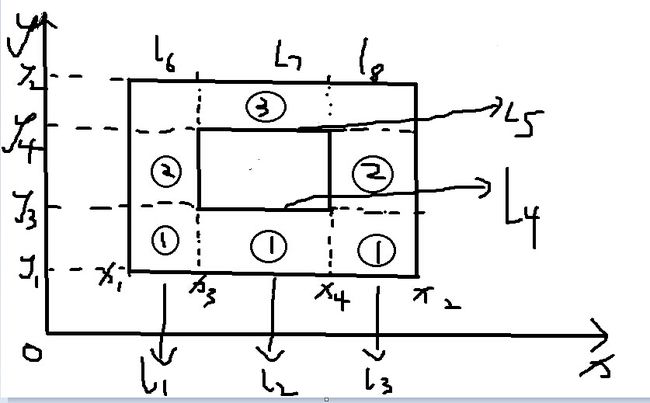
就是给你n个“回”字形的海报,矩形中间挖掉一个小矩形, n个海报贴在窗户上,下面给出n行坐标,每行坐标为(x1,y1)(大矩形左下角)、(x2,y2)(大矩形左上角)、(x3,y3)(小矩形左下角)、(x4,y4)(小矩形左上角) 四个坐标。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
#define N 50017
#define ll root*2
#define rr root*2+1
#define mid (a[root].l+a[root].r)/2
struct Line
{
__int64 l, r;
int h;//高度
int flag;//若该扫描线属于矩形的下边的横边,则叫做入边,值为1,若属于矩形的上边的横边,则叫做出边,值为-1
Line(int a=0,int b=0,int c=0,int d=0):l(a),r(b),h(c),flag(d) {}
} line[N*8];
struct node
{
__int64 l, r;
__int64 cover;//表示某x轴坐标区间内是否有边覆盖
__int64 len;//区间覆盖边长度
} a[N*8];
bool cmp(Line a,Line b)
{
return a.h < b.h;
}
void build(__int64 left,__int64 right,int root)
{
a[root].l = left;
a[root].r = right;
a[root].cover = 0;
a[root].len = 0;
if(left == right)
return;
build(left,mid,ll);
build(mid+1,right,rr);
}
void pushup(int root)
{
if(a[root].cover)
{
a[root].len = a[root].r-a[root].l+1;
}
else if(a[root].l == a[root].r)
{
a[root].len = 0;
}
else
{
a[root].len = a[ll].len+a[rr].len;
}
}
void update(__int64 left,__int64 right,__int64 val,int root)
{
if(left > right)
return;
if(a[root].l==left && a[root].r==right)
{
a[root].cover+=val;//插入或删除操作直接让cover[]+=flag。当cover[]>0时,该区间一定有边覆盖。
pushup(root);
return;
}
if(right <= mid)
update(left,right,val,ll);
else if(left > mid)
update(left,right,val,rr);
else
{
update(left,mid,val,ll);
update(mid+1,right,val,rr);
}
pushup(root);
}
int main()
{
int n, i, k;
while(scanf("%d",&n) && n)
{
k = 0;
__int64 x1, y1, x2, y2, x3, y3, x4, y4;
for(i = 0; i < n; i++)
{
scanf("%I64d%I64d%I64d%I64d%I64d%I64d%I64d%I64d",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);
//本题采用平行x轴的扫描线从下往上扫描
line[k++] = Line(x1,x3,y1,1); //把图中的边用line存起来以便排序
line[k++] = Line(x1,x3,y2,-1);
line[k++] = Line(x4,x2,y1,1);
line[k++] = Line(x4,x2,y2,-1);
line[k++] = Line(x3,x4,y1,1);
line[k++] = Line(x3,x4,y3,-1);
line[k++] = Line(x3,x4,y4,1);
line[k++] = Line(x3,x4,y2,-1);
}
build(0, N*2, 1);
sort(line,line+k,cmp);
__int64 ans = 0;
for(i = 0; i < k-1; i++)
{
update(line[i].l,line[i].r-1,line[i].flag,1);//每插入一次就算一次 ,相对应的边在线段树中会抵消
ans+=(line[i+1].h-line[i].h)*a[1].len;//高 X 低
}
printf("%I64d\n",ans);
}
return 0;
}