【Python】用zip函数求欧氏距离、余弦相似度
首先欧氏距离，如此高大上的名称，其实大家都学过的也就是坐标系，或者说是N维向量坐标系的两点之间的距离^_^。也被称作“欧几里得度量”。
在二维坐标系，公式是这样：
在N维坐标是，公式就是：
而余弦相似度，就是两个向量的夹角余弦值，这个数值常用来评估他们的相似度，具体的公式如下：
，换算成具体的数值就是：
也就是说具体为两个向量的点乘积（数量积、内积）除于各自的模之积
当然，本文不是来介绍数学，是介绍怎么用python快速地，用几行的代码就搞掂这个求解。
首先要先介绍python的zip函数，其作用是将同长度的数组tuple（小括号表示的东东）、列表list（中括号表示的东东）的各项组成一个新的由tuple组成的例子，
还是直接上代码吧，比如下述的一段代码：
#-*-coding:utf-8-*- x=[1,2,3]; y=[4,5,6]; z=[7,8,9]; print zip(x,y,z);
运行结果如下：
这样，有了zip函数就可以为我们同时遍历两个数组、列表List的写作提供了方便。for a,b,c in zip(x,y,z)就成了foreach List x,y,z，也就是对于x,y,z的第i项怎么怎么样。
因此，上面的N维向量的欧式距离的求解是变成这样：
#-*-coding:utf-8-*-
def distance(vector1,vector2):
d=0;
for a,b in zip(vector1,vector2):
d+=(a-b)**2;
return d**0.5;
v1=(1,1,1);
v2=(-1,-1,-1);
print distance(v1,v2);
v3=(1,1);
v4=(-1,-1);
print distance(v3,v4);
运行结果如下：
上面的结果一个是 两倍根号3，另一个是两倍根号2。
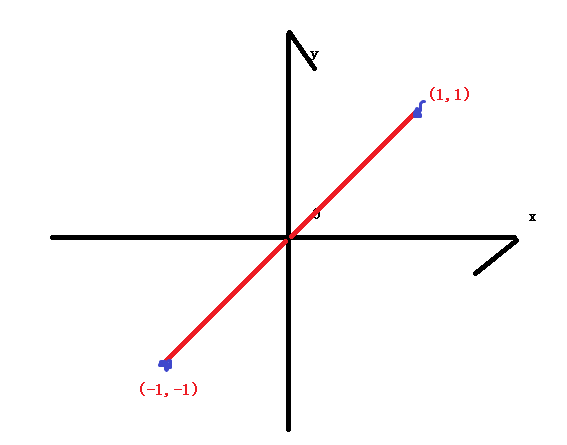
结果很显然是对的，比较(1,1)与(-1,-1)两点距离如下图就是两倍根号2。
余弦相似度同理，根据公式我们可以得到如下的程序：
#-*-coding:utf-8-*-
def cos(vector1,vector2):
dot_product = 0.0;
normA = 0.0;
normB = 0.0;
for a,b in zip(vector1,vector2):
dot_product += a*b
normA += a**2
normB += b**2
if normA == 0.0 or normB==0.0:
return None
else:
return dot_product / ((normA*normB)**0.5)
v1=(1,1);
v2=(-1,-1);
print cos(v1,v2);
v3=(0,1,1);
v4=(0,-1,1);
print cos(v3,v4);
运行结果如下：
很显然，你从我徒手搞出那个坐标系草图就可以看出v1=(1,1)与v2=(-1,-1)是两个互为平行，从原点反方向延伸出来的两个向量，夹角显然为180度，cos 180度=-1这很正确。
之后v3=(0,1,1)与v4=(0,-1,1)是三维坐标系上互为垂直的两个向量，cos 90度=0，这是显然的。
这可以说明v1与v2两个向量简直就是两个不可调和的矛盾，而v3与v4则是毫无关系的两个向量，你可以这样理解。